1. 時系列解析とは何?
いきなりですが、時系列解析 (時系列分析ともいう) とはなんでしょうか?weblio辞書では下記のように説明がされていました。
じけいれつ‐ぶんせき【時系列分析】
ある対象に関する数量の継続的な時間変動を分析し、将来の予測に役立てる手法。株価・為替レート・消費需要・気温や雨量などの自然現象について、その変動の傾向・周期・不規則なふるまいなどを、解析的・統計的・確率的な手法を用いて分析することを指す。
weblio辞書
さて、この無味乾燥とした辞書的説明に具体例を添えながら、時系列解析のイメージをざっくりと掴んでいきましょう。
weblio辞書の説明は
- 「ある対象に関する数量の継続的な時間変動」を
- 分析したり
- 予測したりする
とざっくり分解できるので、この3項目のそれぞれ具体的なイメージが湧くように具体例を添えながら説明していきます。
1.1「ある対象に関する数量の継続的な時間変動」とは?
まず、「ある対象に関する数量の継続的な時間変動」を時系列データといいます。時系列解析では、この時系列データと呼ばれるデータのみを扱います。
説明が抽象的過ぎて、何も頭に入ってこないので、具体例を用意しました。
例えば、下記のような気温データなどが代表的な時系列データです。抽象具体を対応付けると、「ある対象(=気候)に関する数量(=気温)の継続的な(=1週間分)の時間変動」となります。
| 日付 | 東京都の平均気温 |
|---|---|
| 2021/11/01 | 16.8 |
| 2021/11/02 | 17.7 |
| 2021/11/03 | 17.1 |
| 2021/11/04 | 15.5 |
| 2021/11/05 | 15.3 |
| 2021/11/06 | 14.9 |
| 2021/11/07 | 15,7 |
ところで、weblio辞書の説明は少しばかり不正確です。正しくは「一定の間隔で観測した、ある対象に関する数量の継続的な時間変動」となります。再度、上記の例に当てはめると、「一定の間隔で(=1日ごとに)観測した、ある対象(=気候)に関する数量(=気温)の継続的な(=1週間分)の時間変動」となります。
時系列データと混同されやすいデータに点過程データがあります。点過程データとは「ある時間間隔ごとの測定ではなく、あるイベントが発生したタイミングで測定されるデータ」のことをいいます。
例えば、地震データなどが代表的な点過程データです。気温データと同様、時間と紐づくデータですが、一定時間間隔で測定されているわけではなく、地震が発生したタイミングでデータが記録されています。
| 発生時刻 | 震源地 | マグニチュード | 最大震度 |
|---|---|---|---|
| 2021/11/24 18:55 | 与那国島近海 | M5.2 | 2 |
| 2021/11/24 17:06 | 岩手県沖 | M4.7 | 3 |
| 2021/11/24 04:25 | 長野県南部 | M3.0 | 2 |
| 2021/11/23 23:52 | 鹿児島湾 | M2.1 | 1 |
| 2021/11/23 20:30 | 四国沖 | M3.6 | 1 |
| 2021/11/23 18:48 | 宮城県沖 | M5.0 | 3 |
| 2021/11/23 08:52 | 千葉県南東沖 | M3.7 | 2 |
時系列解析では、上記のような点過程データは対象としません。(点過程データの解析を広く時系列解析に含める流儀もありますが)
分析対象として、時系列データと点過程データを明確に分ける理由は、この2つのデータを分析する目的に違いがあり、それゆえに分析方法が異なるためです。
| データ区分 | 分析する目的 |
|---|---|
| 時系列データ | データが時間と共にどのように変化するか知りたい |
| 点過程データ | あるイベントがいつ発生するか知りたい |
1.2 「分析する」とは?
「分析する」は、「記述する」と「モデリングする」という2段階のステップで構成されています。(これは時系列解析に限った話でない)
以下で、具体例で確かめながら「分析する」とは何か理解していきましょう。
(時系列データではないですが) 具体例として下記の数値の羅列を分析してみます。
2, 6, 3, 1, 2, 6, 5, 3, 5, 5, 3, 1, 2, 2, 2, 6, 1, 3, 6, 6■「記述する」
「記述する」とは、得られたデータから特徴的な量を抽出する行為です。要は、データを色々と整理してみて「何か特徴ないかな~?」と根掘り葉掘り調べるということです。
ちなみに、「記述」ステップで得られるデータの特徴量のことを(記述)統計量といいます。
例えば、このデータの平均値は 3.5 で、最大値は 6 で、最小値は 1 ですが、これらはすべてデータの特徴を表しているので、(記述)統計量と言えます。
このように統計量を調べていくと、ただの数字の羅列に見えたデータに、何かしらの傾向があるということが分かってきます。
「1から6までの値しかでないみたいだな~」
「平均が3.5ということは、もしかしたら1から6が満遍なくでるのかな~?そうとも限らないかな~?散らばり具合も調べてみないと分かりませんな」
このようにして、データから特徴量を抽出して、データ全体の傾向を掴むのが「記述する」というステップになります。
■「モデリングする」
「記述する」ことで、得られたヒントを元に、そのデータを吐き出したであろう「確率モデル」に当たりをつけるのが、「モデリングする」というステップです。
さて、いきなり登場した「確率モデル」とはなんでしょうか?確率モデルは、ある規則の則ってランダムに数値を吐き出すマシン のようなものです。

例えば、サイコロの出目について考えてみましょう。
サイコロは、「1から6以外の値は出さない」、「1から6までの数値をどれも同じくらいの頻度で出す」などの規則に則って、ランダムに数値を吐き出します。
実は、サイコロの出目のような数値を吐き出すマシンを数式だけで表現することができます。
$$ サイコロの出目を吐き出すマシンの数式表現: p(x_1,…,x_6) = \prod_{i=1}^{6}\Bigl(\frac{1}{6} \Bigl )^{x_i} $$
こんな感じで、 ある規則の則ってランダムに数値を吐き出すマシン (または、それらマシンを組み合わせたもの) を数式表現したものが「確率モデル」だと思ってください。ちなみに、上記の「 サイコロの出目を吐き出すマシンの数式表現 」のことを「カテゴリカル分布 (の一例)」といいます。
例えば、記述ステップのヒントから「1から6しか出ないし、平均3.5だしカテゴリカル分布から吐き出されたんじゃない??」と、このデータの背後にある確率モデルに当たりをつけたとします。
このように観測されたデータを吐き出したであろうシステムに当たりをつける行為を「モデリング」といいます。
(実際、このデータは私がサイコロを20回振って出た目を記録したものなので、妥当な推測です。)
そして、研究者たちがこれまでにたくさんの「データ吐き出しマシン=確率モデル」を作成してくれているので、まずはどんなモデルがあるのか学習する必要があります。
今後、ARモデル、ARMAモデルやARCHモデルなど、○○モデルという名のついたものを何個か紹介していきますが、それらに対して「時系列データを吐き出すマシン」というイメージを念頭に置くと、それらが何者が理解しやすいでしょう。
また、今回のサイコロの例では、「背後にある確率モデルはカテゴリカル分布だ!」と、短絡的に結論付けましたが、本来はたくさんの確率モデルを検討して、どの確率モデルが最も妥当だと言えるか確認する必要があります。確率モデルの妥当性を判定する基準として「赤池情報量基準 (AIC)」、「ベイズ情報量基準 (BIC)」といった量が代表的です。これらについても、本シリーズで説明していきます。
1.3 「予測する」とは?
さて、最後に「予測する」の説明をします。前段階の「分析する」でデータの背後にある「データ吐き出しマシン」に当たりをつけたので、その仮定の下でなら、これから吐き出されるデータに関しても何かしらの予測ができそうです。
引き続き、サイコロの例で考えると、
「(もしこのデータがサイコロの出目の確率モデルから吐き出されているとしたら) これから1が10回連続してでる確率が低そうだな」
「(もしこのデータがサイコロの出目の確率モデルから吐き出されているとしたら) これから吐き出される数値の平均は3.5くらいになる確率が高いだろうな」
など、「絶対こうなる!」とは断言できないけれど、「こういうことは起きやすそう!起きにくそう!」といったような未来に起こることの確率的な言及はできそうです。
まさに、これが「予測する」ということです。
2. 時系列モデルとは
先で述べた通り、世の中のランダムに見える現象の裏には、確率モデルが潜んでいると考えて、現象を分析することが時系列解析を含む統計解析の基本姿勢でした。確率モデルの中で、特に時系列データを吐き出すものを時系列モデルと呼びます。この章では、時系列モデルについてもう少し具象化していきます。
2.1 時系列モデルの雰囲気を掴む
時系列モデルは、確率過程 \( \{y_t\}_{t\in T} \) の形式で表されます。確率過程とは、時刻 \(t\) で添え字づけられた確率変数の集まりのことです。
確率変数とは、数値吐き出しマシン単体のことを指します。したがって、確率過程とは、各時刻ごとに担当の数値吐き出しマシンがあり、それらが集まったものとでも言いましょうか。
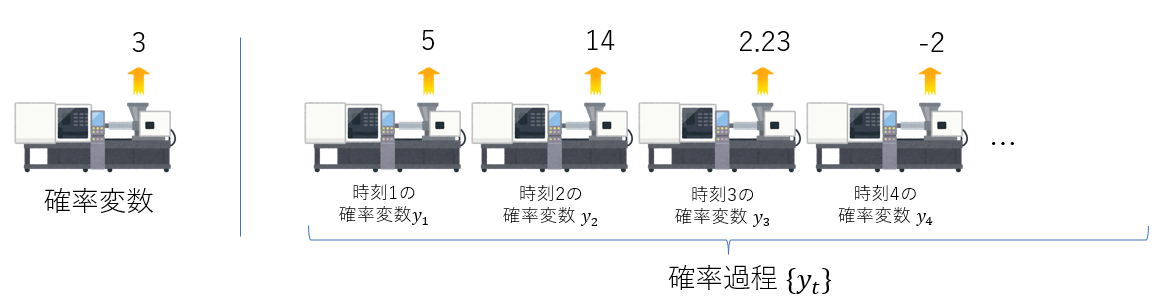
人には見えない世界で、横並びになった「数値吐き出しマシン」が左からポンポン数値を吐き出されます。その吐き出された数値が、時間の経過とともに現実世界に出現する、と考えるわけです。
さて、ただ単に「数値吐き出しマシン」を横並びにしただけでは、時間の経過とともに個々のマシンが好き勝手数値を吐き出すだけです。自分以外のマシンが吐き出した数値には目も向けず、自由奔放に数値を吐き出してしまいます。
しかし、現実に現れる時系列データは、同じ並びにあるデータの影響を受けることがほとんどです。
例えば、最高気温が40℃を記録した次の日に、右隣にあるマシン (つまり、次の日のマシン) がそれを無視して好き勝手に-10℃を吐き出すことはないでしょう (天変地異でも起こらない限り)。 逆に、その半年分右隣のマシン (つまり、真冬のマシン) が40℃を出すこともないでしょう。( 個人的には冬が嫌いなので、そうなってくれたら嬉しいな)
このように、現実の時系列データを吐き出すマシンは、横並びの者同士で影響を受けあっているので、これから構築する時系列モデルも横並びのマシンを色々な方法で接続しあって、影響を受け合うようなマシンにしたいわけです。
つまり時系列モデルを構築するとは、横並びになった『単体マシン ( = 確率変数) 』1つ1つをつなぎ込んで、マシン同士が影響を与え合いながら数値を吐き出す『横並びマシン ( = 確率過程) 』を作り上げるということに他なりません。
過去に偉大な研究者たちによって、さまざまなマシンの繋ぎ込み方法 (マシン同士を影響のさせ合う方法) が提案されています。私たちは、まずその代表的なつなぎ込み方を学ぶというわけです。
2.2 時系列データの基本統計量
横並びマシン ( = 時系列モデル) の性能指標を紹介しておきます。
■ 横並びになっている個々のマシンの性能指標
- 時刻 \(t\) における時系列データ \(y_t\) の平均 \(\mu_t = \textrm{E}[y_t]\)
- 時刻 \(t\) における時系列データ \(y_t\) の分散 \(\sigma_t^2 = \textrm{Var}[y_t] = \textrm{E}[(y_t-\mu_t)^2]\)
- 時刻 \(t\) における時系列データ \(y_t\) の標準偏差 \(\sigma_t = \sqrt{\textrm{Var}[y_t]}\)
これらは、通常の統計学でも登場するお馴染み統計量なので、簡潔に説明すると、時刻 \( t \) における時系列データ \(y_t\) が平均的にどれくらいの値を吐き出すかを表した値が平均 \(\mu_t\) で、吐き出す値がその平均からどれくらい散らばりうるか表した指標が分散 \( \sigma_t^2\) や標準偏差 \( \sigma_t \) です。
■ マシン同士の影響を評価する指標
ここでは、マシン同士が吐き出す値がどのくらい似た値を吐き出すか (似ないか、はたまた天邪鬼の様に反対の方向の値をとるか) を測る指標を紹介します。
- 時刻 \( t \) における \( k \) 次の自己共分散
$$ \gamma_{k,t} = \textrm{Cov}[y_t, y_{t-k}] = \textrm{E}[(y_t-\mu_t)(y_{t-k}-\mu_{t-k}) ] $$
これは、時刻 \(t\) のマシンと、そこから \(k\) 時点前である時刻 \(t-k\) のマシンとの関係を表しています。
\( \gamma_{k,t} \) が正の値のとき、時刻 \( t \) における時系列データ \(y_t\) とそこから \( k \) 時間前の時刻 \(t-k\) における時系列データ \(y_{t-k}\) はそれぞれの平均を基準にして、同じ方向に動く傾向があると言えます。(ちなみに、0なら関係なさそう、負なら反対方向に動きそう)
ただし自己共分散には、値が単位に依存してしまうという問題点があるため、自己共分散を正規化した ( = 単位の影響を受けないようにした) 自己相関係数という指標が用意されています。例えば、気温データを摂氏と華氏で2通りで表したとすると、自己共分散が異なる値 (正負は一致する) をとります。しかし、単位のせいで、影響度合いを表す数値が変化するのは、不便です。単位は表記を変えるだけで、それが指す元の数量は変わっていないのですから。(6kg と 6000g は表記は違うが、同じ数量を指している。)
- 時刻 \( t \) における \( k \) 次の自己相関係数
$$ \rho_{k,t} = \textrm{Corr}[y_t, t_{t-k}] = \frac{\textrm{Cov}[y_t, t_{t-k}]}{\sqrt{\textrm{Var}[y_t]\textrm{Var}[y_{t-k}] }} = \frac{\gamma_{k,t}}{\sqrt{\gamma_{0,k}\gamma_{0,t-k}}} $
Comments are closed