1. 状態空間モデル

状態空間モデルは、2つの確率過程からなります。１つは潜在変数・状態変数・隠れ変数といわれるもので、これは直接観測できないがマルコフ連鎖に従う変数だとモデリングされます。例えば景気の良し・悪し等、概念として存在するけれど直接は観測できないものを想像してください。２つめは観測値で、これは直接観測できるもの、つまりデータです。ただし変数に依存して観測されるとします。今の例ですと、例えば株価などを想像してください。意味としては株価は景気の良し悪しに依存して決まるということです。この観測値にも「状態変数で条件づけると過去の自分自身とは独立となる」という仮定を置きます。

1.1. 状態空間モデルの定式化

\( t = 1,2,…,T \) を時刻とします。\( d_{ \boldsymbol{ x } } \) 次元の状態ベクトル \( d_{ \boldsymbol{ y } } \) 次元の観測ベクトル \( \boldsymbol{ y }_t \) というベクトル値変数を導入します。このとき、状態空間モデルの一般的な表現は以下のようになります。

$$
\begin{align}
\boldsymbol{ x }_t &= F_t ( \boldsymbol{ x }_{ t-1 } , \boldsymbol{ v }_t ) \tag{1} \\
\boldsymbol{ y }_t &= H_t ( \boldsymbol{ x }_t , \boldsymbol{ w }_t ) \tag{2} \\
\boldsymbol{ x }_0 &\sim \mathcal{ N } ( \boldsymbol{ \mu }_0 , V_0 ) \tag{3} \\
\boldsymbol{ v }_t &\sim \mathcal{ N } ( \boldsymbol{ 0 } , Q_t ) \tag{4} \\
\boldsymbol{ w }_t &\sim \mathcal{ N } ( \boldsymbol{ 0 } , R_t ) \tag{5}
\end{align}
$$

(1)式はシステムモデル、(2)式は観測モデル、\( \boldsymbol{ v }_t \) と \( \boldsymbol{ w }_t \) はそれぞれシステムノイズ、観測ノイズと呼ばれます。 グラフィカルモデルで表すと次のようになります。

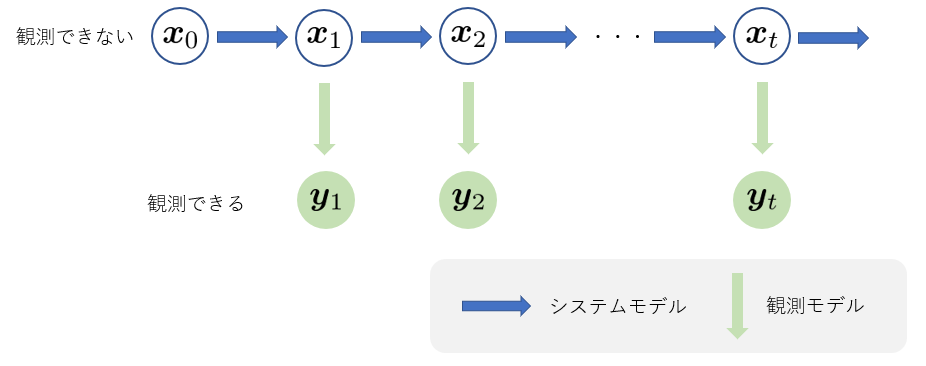
グラフィカルモデルを見れば一目瞭然ですが、下記のような条件付き独立性が成り立ちます。

$$
\begin{align}
p ( \boldsymbol{ x }_t | \boldsymbol{ x }_{ 1 : t-1 } , \boldsymbol{ y }_{ 1 : t-1 } ) &= p ( \boldsymbol{ x }_t | \boldsymbol{ x }_{ t-1 } ) \tag{6} \\
p ( \boldsymbol{ y }_t | \boldsymbol{ x }_{ 1 : t } , \boldsymbol{ y }_{ 1 : t-1 } ) &= p ( \boldsymbol{ y }_t | \boldsymbol{ x }_{ t } ) \tag{7}
\end{align}
$$

要するに、状態系列はマルコフ過程であり、観測値はそのときの状態によってのみ決まることを意味しています。

2. 逐次的な状態推定法の一般論

今、時刻 \( j \) までに得られた観測全体を、

$$ y_{1:j} \equiv \{ y_1,…,y_j \} \tag{8}$$

と表すことにします。

状態空間モデルにおけるある時点 \( t \) の状態 \( \boldsymbol{ x }_t \) について、ある一定区間の観測 \( y_{1:j} \) を得た下での推定について考えます。これは、\( p(\boldsymbol{x}_t | y_{1:j} ) \) という条件付き周辺分布の推定を得ることに対応します。この条件付き周辺分布は観測時点 \( j \) と推定する状態の時点 \( t \) との関係により、次の３種類に分類されます。

• \( t > j \) の場合：予測分布 (特に, \(t=j+1\) のときを一期先予測分布と呼びます)
• \( t = j \) の場合：フィルタリング分布
• \( t < j \) の場合：平滑化分布

予測分布を推定することを予測と呼びます。同様に、フィルタリング分布、平滑化分布を推定することをそれぞれフィルタリング、平滑化と呼びます。

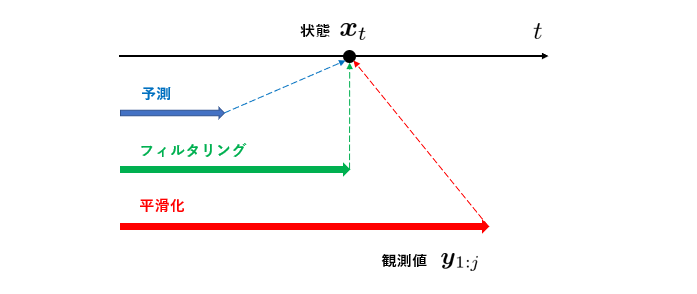
さて、以下でこの平滑化・フィルタリング・予測を “逐次的に” 実行する方法を解説します。

( “逐次的に” と強調したのは、“バッチ処理的 (一括処理的) に” 実行する方法もあるからです。今回は、バッチ処理的な方法は解説しません。)

2.1. フィルタリング分布の逐次計算

時刻 \(t-1\) のフィルタリング分布 \( p(\boldsymbol{x}_{t-1} | y_{1:t-1} ) \) が与えられているとします。これから時刻 \(t\) のフィルタリング分布 \( p(\boldsymbol{x}_{t} | y_{1:t} ) \) を求めるのが、逐次ベイズフィルタリングです。逐次ベイズフィルタは、一期先予測とフィルタリングも２つのステップを逐次的に行います。

STEP1. 一期先予測

★方針：『フィルタリング分布 \( p(\boldsymbol{x}_{t-1} | y_{1:t-1} ) \) から一期先予測分布 \( p(\boldsymbol{x}_{t} | y_{1:t-1} ) \) を求める』

$$
\begin{align}
p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } )
&= \int p ( \boldsymbol{ x }_t | \boldsymbol{ x }_{ t-1 } , y_{ 1 : t-1 } )
p ( \boldsymbol{ x }_{ t-1 } | y_{ 1 : t-1 } ) d \boldsymbol{ x }_{ t-1 } \tag{9} \\
&= \int p ( \boldsymbol{ x }_t | \boldsymbol{ x }_{ t-1 } )
p ( \boldsymbol{ x }_{ t-1 } | y_{ 1 : t-1 } ) d \boldsymbol{ x }_{ t-1 } \tag{10}
\end{align}
$$

(9)式から(10)式の変形には、「状態のマルコフ性」を用いています。(10)式に着目すると、\( p(\boldsymbol{x}_{t-1} | y_{1:t-1} ) \) は所与のフィルタリング分布であり、\( p ( \boldsymbol{ x }_t | \boldsymbol{ x }_{ t-1 } ) \) はモデルが規定する分布ですから、こちらも所与です。したがって、\( p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) \) が求められたことになります。

STEP2. フィルタリング

★方針：『一期先予測分布 \( p(\boldsymbol{x}_{t} | y_{1:t-1} ) \) からフィルタリング分布 \( p(\boldsymbol{x}_{t} | y_{1:t} ) \) を求める』

$$
\begin{align}
p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } )
&\propto p ( y_t | \boldsymbol{ x }_t , y_{ 1 : t-1 } ) p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) \tag{11} \\
&= p ( y_t | \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) \tag{12} \\
\end{align}
$$

$$
\begin{align}
\Longrightarrow~~~ p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) =
\frac{
p ( y_t | \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } )
}{
\int p ( y_t | \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) d \boldsymbol{ x }_t
} = \frac{
p ( y_t | \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } )
}{
p ( \boldsymbol{ y }_t | \boldsymbol{ y }_{1:t-1} )
} \tag{13}
\end{align}
$$

(11)式はベイズの定理、 (12)式は「観測の条件付き独立性」により導かれます。最後に正規化したのが(13)式ですが、\( p ( y_t | \boldsymbol{ x }_t ) \) はモデルが規定する分布で、\( p ( \boldsymbol{ x }_t | y_{ 1 : t-1 } ) \) はSTEP1.で得られた一期先予測分布ですから、どちらも所与です。しがたって、\( p ( \boldsymbol{ x }_t | y_{ 1 : t } ) \) が求められたことになります。

2.2. 予測分布の逐次計算

さて、いま時刻 \( j \) までの観測全体 \( y_{ 1 : j } \) が得られているとすると、逐次ベイズフィルタリングにより、\( p ( \boldsymbol{ x }_j | y_{ 1 : j } ) \) までのフィルタリング分布を求めることができます。一方、予測分布の計算、すなわち時刻 \( j \) より先の状態の分布を計算するには、上記STEP1 (一期先予測) の計算方法を応用すればよいわけです。

★方針：『\( k \) 期先予測分布 \( p(\boldsymbol{x}_{j+k} | y_{ 1:j } ) \) から \( k+1 \) 期先予測分布 \( p(\boldsymbol{x}_{j+k+1} | y_{ 1:j } ) \) を求める』

式を見やすくするために、\( t = j+k \) とおく。

$$
\begin{align}
p ( \boldsymbol{ x }_{ t+1 } | y_{ 1 : j } )
&= \int p ( \boldsymbol{ x }_{ t+1 } | y_{ 1 : j } , \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : j } ) d \boldsymbol{ x }_{ j+k } \tag{14} \\
&= \int p ( \boldsymbol{ x }_{ t+1 } | \boldsymbol{ x }_t ) p ( \boldsymbol{ x }_t | y_{ 1 : j } ) d \boldsymbol{ x }_t \tag{15}
\end{align}
$$

上記の計算を繰り返すことで、予測分布からさらにその一時点先の予測分布が逐次的に計算されていきます。

予測分布を使って、さらにその先の状態を予測することを繰り返すので、先の状態になればなるほど、精度が悪い推定になるのは容易に想像できます。

2.3. 平滑化分布の逐次計算

時刻 \( j \) までの観測全体 \( y_{ 1 : j } \) が得られていると仮定して、2.1.では時刻 \( j \) までの各時刻のフィルタリング分布を導出し、2.2.では時刻 \( j \) より先の状態の分布 (=予測分布) を計算してきました。

いま、時刻 \( j \) よりも前の時刻 \( t ~ \small{(<j)} \) の状態分布として、フィルタリング分布 \( p (\boldsymbol{ x }_t | y_{ 1:t }) \)が得られています。しかし、このフィルタリング分布は観測全体 \( y_{ 1 : j } \) のうち、\( y_{ 1 : t } \) の観測結果しか利用しておらず、残りの \( y_{ t+1 : j } \) の情報を反映していません。(実にもったいない)

そこで、 未反映の観測結果 \( y_{ t+1 : j } \) を時刻 \( t~ \small{(<j)} \) のフィルタリング分布に反映することで分布を更新します。こうして得られる時刻 \( t~ \small{(<j)} \) の状態分布が平滑化分布となるわけです。得られている観測値をフル活用している分、フィルタリング分布よりも精度の高い状態推定が行えることになります。

では、実際に平滑化分布を導出していきます。時刻 \( j \) から時間逆方向に逐次的にフィルタリング分布の更新を行う作戦を取ります。

★方針：『平滑化分布 \( p(\boldsymbol{x}_{t+1} | y_{ 1:j } ) \) から一つ前時点の平滑化分布 \( p(\boldsymbol{x}_t | y_{ 1:j } ) \) を求める』

ここは導出過程を丁寧に記述すると、結構長くなってしまうので、割愛させていただきます。結果の関係式だけ下に記します。

$$
\begin{align}
p ( \boldsymbol{ x }_t | y_{ 1 : j } )
= p ( \boldsymbol{ x }_t | y_{ 1 : t } )
\int \frac{
p ( \boldsymbol{ x }_{ t+1 } | y_{ 1 : j } )
p ( \boldsymbol{ x }_{ t+1 } | \boldsymbol{ x }_t )
}{
p ( \boldsymbol{ x }_{ t+1 } | y_{ 1 : t } )
}
d \boldsymbol{ x }_{ t+1 } \tag{16}
\end{align}
$$

このようにして観測全体を利用した平滑化分布を求めることを、固定区間平滑化と呼びます。

3. 線形ガウス状態空間モデルとカルマンフィルター

一般的に、状態空間モデルのフィルタリング分布や予測分布の計算は、CH.2で見たように、複雑な積分を伴うため解析的に解くことができません….しょんぼり。MCMCなどの数値近似が必要になるということです。しかし、線形ガウス状態空間モデルという特別なケースにおいては、なんと解析的に解けます！その解法をカルマンフィルター(カルマン予測・カルマン平滑化)といいます。( MCMCなどの数値近似による解法については、今回は扱いません)

3.1. 線形ガウス状態空間モデル

一般化状態空間モデルにおいて、\( F_t , G_t \) が線形であり、状態・観測がともに正規分布に従うとき、とくに線形ガウス状態空間モデルと呼ばれます。具体的な式に書き下すと、

$$
\begin{align}
\boldsymbol{ x }_t &= F_t \boldsymbol{ x }_{ t-1 } + \boldsymbol{ v }_t \tag{17} \\
\boldsymbol { y }_t &= G_t \boldsymbol{ x }_t + \boldsymbol{ w }_t \tag{18} \\
\end{align}
$$

となります。ここで、\( F_t \) は \( d_x \times d_x \) 行列、\( G_t \) は \( d_y \times d_x \) 行列でそれぞれシステム行列、観測行列と呼ばれます。\( \boldsymbol{v}_t \) と \( \boldsymbol{w}_t \) はそれぞれ \( \mathcal{N}(\boldsymbol{0}, Q_t), \mathcal{N}(\boldsymbol{0},R_t) \) に従うとします。

線形ガウス状態空間モデルでは、正規分布の正規性から対象となる分布はすべて正規分布になります。したがって、平均ベクトルと共分散行列さえ計算できれば分布が特定できるわけです。

3.1. 下準備

状態 \(\boldsymbol{x}_t\) の条件付き平均と共分散行列に対して、以下のような記法を用意します。

$$
\begin{align}
\boldsymbol{x}_{t|j} &:= \textrm{E}[\boldsymbol{x}_t|\boldsymbol{y}_{1:j}] \tag{19} \\
V_{t|j} &:= \textrm{E}[( \boldsymbol{x}_t – \boldsymbol{x}_{t|j} )( \boldsymbol{x}_t – \boldsymbol{x}_{t|j} )^T] \tag{20}
\end{align}
$$

さて、以下では、カルマンフィルターの計算方法を紹介しながら、pythonを用いてカルマンフィルタークラスを実装していきます。まず、線形ガウス状態空間モデルは

• システム行列
• 観測行列
• システムノイズの共分散行列
• 観測ノイズの共分散行列
• 状態の初期値の平均ベクトル
• 状態の初期値の共分散行列

で規定されるので、初期化の際にこれらをセットすることにします。実装に関しては、システム行列・観測行列・システムノイズの共分散行列・観測ノイズの共分散行列が共に時間に依らないシンプルなケースを書きます。

import numpy as np

class KalmanFilter(object):
    def __init__(self, system_matrix, observation_matrix,
                 system_cov, observation_cov,
                 initial_state_mean, initial_state_cov,):
        self.system_matrix = np.array(system_matrix)
        self.observation_matrix = np.array(observation_matrix)
        self.system_cov = np.array(system_cov)
        self.observation_cov = np.array(observation_cov)
        self.initial_state_mean = np.array(initial_state_mean)
        self.initial_state_cov = np.array(initial_state_cov)

3.2. カルマンフィルター

このパートは、「2.1.フィルタリング分布の逐次計算」の線形ガウス状態空間モデルにおける解析的な解法の説明となります。

STEP1. 一期先予測

★方針：『フィルタリング分布 \( p(\boldsymbol{x}_{t-1} | y_{1:t-1} )=\mathcal{N}(\boldsymbol{x}_{t-1|t-1},V_{t-1|t-1}) \) から一期先予測分布 \( p(\boldsymbol{x}_{t} | y_{1:t-1} )= \mathcal{N}(\boldsymbol{x}_{t|t-1},V_{t|t-1}) \) を求める』

$$
\begin{align}
\boldsymbol{x}_{t|t-1} &= F_t \boldsymbol{x}_{t-1|t-1} \tag{21} \\
V_{t|t-1} &= F_t V_{t-1|t-1} F_t ^T + Q_t \tag{22}
\end{align}
$$

def filter_predict(self, current_state_mean, current_state_cov):
    predicted_state_mean = self.system_matrix @ current_state_mean
    predicted_state_cov = (
        self.system_matrix
        @ current_state_cov
        @ self.system_matrix.T
        + self.system_cov
    )
    return (predicted_state_mean, predicted_state_cov)

STEP2. フィルタリング

★方針：『一期先予測分布 \( p(\boldsymbol{x}_{t} | y_{1:t-1} )=\mathcal{N}(\boldsymbol{x}_{t|t-1},V_{t|t-1}) \) から一期先予測分布 \( p(\boldsymbol{x}_{t} | y_{1:t} )= \mathcal{N}(\boldsymbol{x}_{t|t},V_{t|t}) \) を求める』

$$
\begin{align}
K_t &= V_{t|t-1} G_t^T ( G_t V_{t|t-1} G_t^T + R_t)^{-1} \tag{23} \\
\boldsymbol{x}_{t|t} &= \boldsymbol{x}_{t|t-1} + K_t (y_t – G_t \boldsymbol{x}_{t|t-1} ) \tag{24} \\
V_{t|t} &= V_{t|t-1} – K_tG_tV_{t|t-1} \tag{25}
\end{align}
$$

def filter_update(self, predicted_state_mean, predicted_state_cov, observation):
    kalman_gain = (
        predicted_state_cov 
        @ self.observation_matrix.T 
        @ np.linalg.inv(
            self.observation_matrix
            @ predicted_state_cov
            @ self.observation_matrix.T
            + self.observation_cov
        )
    )
    filtered_state_mean = (
        predicted_state_mean
        + kalman_gain
        @ (observation
           - self.observation_matrix
           @ predicted_state_mean)
    )
    filtered_state_cov = (
        predicted_state_cov
        - (kalman_gain
           @ self.observation_matrix
           @ predicted_state_cov)
    )
    return (filtered_state_mean, filtered_state_cov)

上記のSTEP1,2を逐次的に実行することで、フィルタリング分布が計算されます。最後に逐次計算部分を実装します。

def filter(self, observations):
    observations = np.array(observations)
    
    n_timesteps = len(observations)
    n_dim_state = len(self.initial_state_mean)
    
    predicted_state_means = np.zeros((n_timesteps, n_dim_state))
    predicted_state_covs = np.zeros((n_timesteps, n_dim_state, n_dim_state))
    filtered_state_means = np.zeros((n_timesteps, n_dim_state))
    filtered_state_covs = np.zeros((n_timesteps, n_dim_state, n_dim_state))
    
    for t in range(n_timesteps):
        if t == 0:
            predicted_state_means[t] = self.initial_state_mean
            predicted_state_covs[t] = self.initial_state_cov
        else:
            predicted_state_means[t], predicted_state_covs[t] = self.filter_predict(
                filtered_state_means[t-1],
                filtered_state_covs[t-1]
            )
        filtered_state_means[t], filtered_state_covs[t] = self.filter_update(
            predicted_state_means[t],
            predicted_state_covs[t],
            observations[t]
        )
    
    return (
        filtered_state_means,
        filtered_state_covs,
        predicted_state_means,
        predicted_state_covs
    )

3.3. カルマン予測

このパートは、「2.2.予測分布の逐次計算」の線形ガウス状態空間モデルにおける解析的な解法の説明となります。

やっていること自体はカルマンフィルタのSTEP1.と何ら変わらないので、メソッドに関しても、 カルマンフィルタのSTEP1. で定義した predictメソッドを利用すればよいです。

★方針：『\( k \) 期先予測分布 \( p(\boldsymbol{x}_{j+k} | y_{ 1:j } ) = \mathcal{N}(\boldsymbol{x}_{j+k|j},V_{j+k|j}) \) から \( k+1 \) 期先予測分布 \( p(\boldsymbol{x}_{j+k+1} | y_{ 1:j } ) = \mathcal{N}(\boldsymbol{x}_{j+k+1|j},V_{j+k+1|j}) \) を求める』

$$
\begin{align}
\boldsymbol{x}_{j+k+1|j} &= F_{ j+k+1 } \boldsymbol{x}_{ j+k |j} \tag{26} \\
V_{ j+k+1 |j} &= F_{ j+k+1 } V_{ j+k|j} F_{ j+k+1 } ^T + Q_{ j+k+1 } \tag{27}
\end{align}
$$

一期先予測の `filter_predict` を用いて、\( k \) 期先までの予測分布を返すメソッドを用意しておきます。

def predict(self, n_timesteps, observations):
    (filtered_state_means,
    filtered_state_covs,
    predicted_state_means,
    predicted_state_covs) = self.filter(observations)

    _, n_dim_state = filtered_state_means.shape

    predicted_state_means = np.zeros((n_timesteps, n_dim_state))
    predicted_state_covs = np.zeros((n_timesteps, n_dim_state, n_dim_state))

    for t in range(n_timesteps):
        if t == 0:
            predicted_state_means[t], predicted_state_covs[t] = self.filter_predict(
                filtered_state_means[-1],
                filtered_state_covs[-1]
            )
        else:
            predicted_state_means[t], predicted_state_covs[t] = self.filter_predict(
                predicted_state_means[t-1],
                predicted_state_covs[t-1]
            )

    return (predicted_state_means, predicted_state_covs)

3.4. カルマン平滑化

このパートは、「2.3.平滑化分布の逐次計算」の線形ガウス状態空間モデルにおける解析的な解法の説明となります。

★方針：『平滑化分布 \( p(\boldsymbol{x}_{t+1} | y_{ 1:T } )=\mathcal{N}(\boldsymbol{x}_{t+1|T},V_{t+1|T}) \) から一つ前時点の平滑化分布 \( p(\boldsymbol{x}_t | y_{ 1:T } )= \mathcal{N}(\boldsymbol{x}_{t|T},V_{t|T}) \) を求める』

$$
\begin{align}
A_t &= V_{t|t} F_{t+1}^T V_{t+1|t} \tag{28} \\
\boldsymbol{x}_{t|T} &= \boldsymbol{x}_{t|t} +A_t( \boldsymbol{x}_{t+1|T} – \boldsymbol{x}_{t+1|t} ) \tag{29} \\
V_{t|T} &= V_{t|t} +A_t(V_{t+1|T}-V_{t+1|t})A_t^T \tag{30}
\end{align}
$$

def smooth_update(self, filtered_state_mean, filtered_state_cov,
                    predicted_state_mean, predicted_state_cov,
                    next_smoothed_state_mean, next_smoothed_state_cov):
    kalman_smoothing_gain = (
        filtered_state_cov
        @ self.system_matrix.T
        @ np.linalg.inv(predicted_state_cov)
    )
    smoothed_state_mean = (
        filtered_state_mean
        + kalman_smoothing_gain
        @ (next_smoothed_state_mean - predicted_state_mean)
    )
    smoothed_state_cov = (
        filtered_state_cov
        + kalman_smoothing_gain
        @ (next_smoothed_state_cov - predicted_state_cov)
        @ kalman_smoothing_gain.T
    )
    return (smoothed_state_mean, smoothed_state_cov)

上記のメソッドを時間逆方向に逐次的に実行することで、すべての平滑化分布が得られます。その平滑化の逐次処理を実装します。

def smooth(self, observations):
    (filtered_state_means,
    filtered_state_covs,
    predicted_state_means,
    predicted_state_covs) = self.filter(observations)

    n_timesteps, n_dim_state = filtered_state_means.shape

    smoothed_state_means = np.zeros((n_timesteps, n_dim_state))
    smoothed_state_covs = np.zeros((n_timesteps, n_dim_state, n_dim_state))

    smoothed_state_means[-1] = filtered_state_means[-1]
    smoothed_state_covs[-1] = filtered_state_covs[-1]

    for t in reversed(range(n_timesteps - 1)):
        smoothed_state_means[t], smoothed_state_covs[t] = self.smooth_update(
            filtered_state_means[t],
            filtered_state_covs[t],
            predicted_state_means[t+1],
            predicted_state_covs[t+1],
            smoothed_state_means[t+1],
            smoothed_state_covs[t+1]
        )
    
    return (smoothed_state_means, smoothed_state_covs)

4. 実際に動かしてみた

ローカルレベルモデルと呼ばれる状態も観測も一次元の簡単なモデルで実験してみます。

$$
\begin{align}
x_t &= x_{t-1} + v_t \tag{31} \\
y_t &= x_t + w_t \tag{32} \\
v_t &\sim \mathcal{N}(0, 1) \tag{33} \\
w_t &\sim \mathcal{N}(0, 10) \tag{34}
\end{align}
$$

4.1. テストデータ生成

np.random.seed(1) # 乱数固定

n_timesteps = 120

system_matrix = [[1]]
observation_matrix = [[1]]
system_cov = [[1]]
observation_cov = [[10]]
initial_state_mean = [0]
initial_state_cov = [[1e7]]


states = np.zeros(n_timesteps)
observations = np.zeros(n_timesteps)
system_noise = np.random.multivariate_normal(
    np.zeros(1),
    system_cov,
    n_timesteps
)
observation_noise = np.random.multivariate_normal(
    np.zeros(1),
    observation_cov,
    n_timesteps
)

states[0] = initial_state_mean + system_noise[0]
observations[0] = states[0] + observation_noise[0]
for t in range(1, n_timesteps):
    states[t] = states[t-1] + system_noise[t]
    observations[t] = states[t] + observation_noise[t]

# 分析するデータ(時刻0から99まで)と予測と比較する用のデータ(時刻100以降)に分けておく
states_train = states[:100]
states_test = states[100:]
observations_train = observations[:100]
observations_test = observations[100:]

生成されたデータを描画しています。青が状態、グレーが観測値を表しています。

import matplotlib.pyplot as plt

upper = 17
lower = -12

fig, ax = plt.subplots(figsize=(16, 4))
ax.plot(np.arange(n_timesteps), states, label=" true state")
ax.plot(np.arange(n_timesteps), observations, color="gray", label="observation")
ax.set_title("simulation data")
ax.set_ylim(lower, upper)
ax.legend(loc='upper left')

4.2. モデル生成と推定

# モデル生成
model = KalmanFilter(
    system_matrix,
    observation_matrix,
    system_cov,
    observation_cov,
    initial_state_mean,
    initial_state_cov
)

# フィルタリング分布取得
filtered_state_means, filtered_state_covs, _, _ = model.filter(observations_train)

# 予測分布取得
predicted_state_means, predicted_state_covs = model.predict(len(states_test), observations_train)

# 平滑化分布取得
smoothed_state_means, smoothed_state_covs = model.smooth(observations_train)

4.3. 結果

import matplotlib.pyplot as plt

upper = 17
lower = -10

T1 = len(states_train)
T2 = len(states_test)

# フィルタリング・予測・平滑化の下側95％点と上側95％点
filtering_lower95 = filtered_state_means.flatten() - 1.96 * filtered_state_covs.flatten()**(1/2)
filtering_upper95 = filtered_state_means.flatten() + 1.96 * filtered_state_covs.flatten()**(1/2)
prediction_lower95 = predicted_state_means.flatten() - 1.96 * predicted_state_covs.flatten()**(1/2)
prediction_upper95 = predicted_state_means.flatten() + 1.96 * predicted_state_covs.flatten()**(1/2)
smoothing_lower95 = smoothed_state_means.flatten() - 1.96 * smoothed_state_covs.flatten()**(1/2)
smoothing_upper95 = smoothed_state_means.flatten() + 1.96 * smoothed_state_covs.flatten()**(1/2)


fig, axes = plt.subplots(nrows=3, figsize=(16, 12))

# フィルタリングと予測
axes[0].plot(np.arange(T1+T2), states, label="true state")
axes[0].plot(np.arange(T1), filtered_state_means.flatten(), color="red", label="filtering")
axes[0].fill_between(np.arange(T1), filtering_lower95, filtering_upper95, color='red', alpha=0.15)
axes[0].plot(np.arange(T1, T1+T2), predicted_state_means.flatten(), color="indigo", label="prediction")
axes[0].fill_between(np.arange(T1, T1+T2), prediction_lower95, prediction_upper95, color="indigo", alpha=0.15)
axes[0].axvline(100, color="black", linestyle="--", alpha=0.5)
axes[0].set_ylim(lower, upper)
axes[0].legend(loc='upper left')
axes[0].set_title("Filtering & Prediction")

# 平滑化
axes[1].plot(np.arange(T1+T2), states, label="true state")
axes[1].plot(np.arange(T1), smoothed_state_means.flatten(), color="darkgreen", label="smoothing")
axes[1].fill_between(np.arange(T1), smoothing_lower95, smoothing_upper95, color='darkgreen', alpha=0.15)
axes[1].axvline(100, color="black", linestyle="--", alpha=0.5)
axes[1].set_ylim(lower, upper)
axes[1].legend(loc='upper left')
axes[1].set_title("Smoothing")

# フィルタリングと平滑化の信頼区間の比較
axes[2].plot(np.arange(T1), filtering_lower95, color='red', linestyle="--", label='filtering confidence interval')
axes[2].plot(np.arange(T1), filtering_upper95, color='red', linestyle="--")
axes[2].fill_between(np.arange(T1), smoothing_lower95, smoothing_upper95, color='darkgreen', alpha=0.3, label='smoothing confidence interval')
axes[2].axvline(100, color="black", linestyle="--", alpha=0.5)
axes[2].set_xlim(-6, 125)
axes[2].set_ylim(lower, upper)
axes[2].legend(loc='upper left')
axes[2].set_title("Confidence interval: Filtering v.s. Smoothing")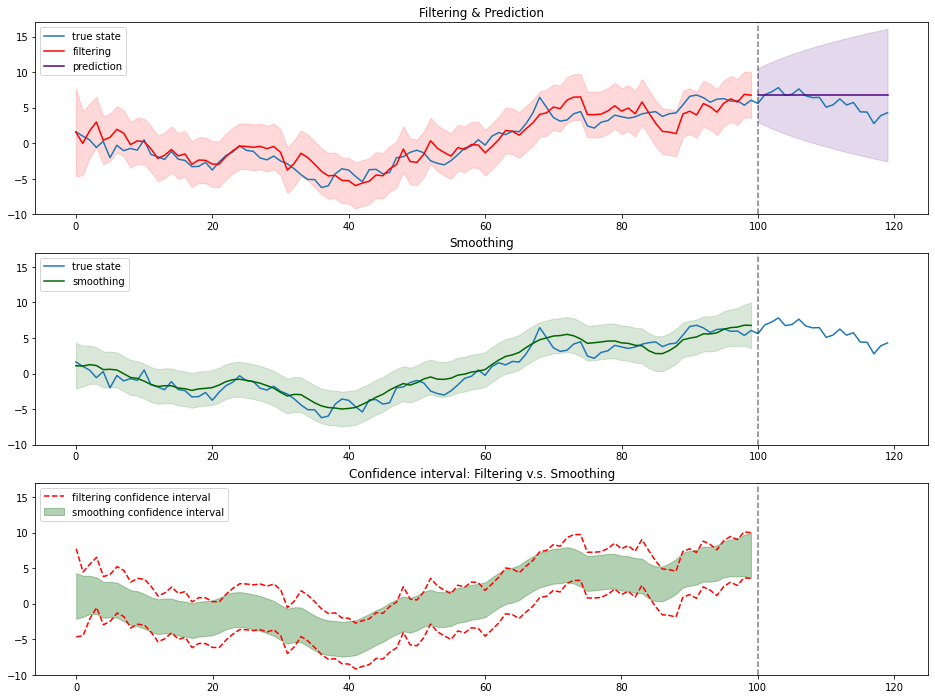

「2.2. 予測分布の逐次計算」で「予測分布を使って、さらにその先の状態を予測することを繰り返すので、先の状態になればなるほど、精度が悪い推定になるのは容易に想像できます。」と述べましたが、実際に時刻が先になればなるほど信頼区間が広がっている様が見て取ります。

「2.3. 平滑化分布の逐次計算」で「得られている観測値をフル活用している分、フィルタリング分布よりも精度の高い状態推定が行えることになります。」と述べましたが、こちらも信頼区間を比較した3つ目の図で確かめられます。