※今回からは、なんの断りもなく確率統計の記号を使用しますが、数式が意味が分からなくても、なんとなく雰囲気を掴めるように心がけました。数学が分からない人はとりあえず数式部分は深く考えず読んでください。興味が湧いたら、数学勉強してみてね!
1. ARモデル
ARモデルは、日本語では自己回帰モデルと呼ばれ、例えるなら、今日の我が身が明日の我が身を作り上げるという、因果律を表現したモデルです。数式にすると、
$$ y_t = c + \phi_1 y_{t-1} + \varepsilon_t,~~~\varepsilon_t \sim \textrm{W.N.}(\sigma^2) $$
のように定式化される。つまるところ、明日の自分 \( y_t \) は今日の自分が明日の自分に与える影響 \( c + \phi_1 y_{t-1} \) と明日起きる偶然 \( \varepsilon_t \) を混ぜ合わせてで出来上がるということです。
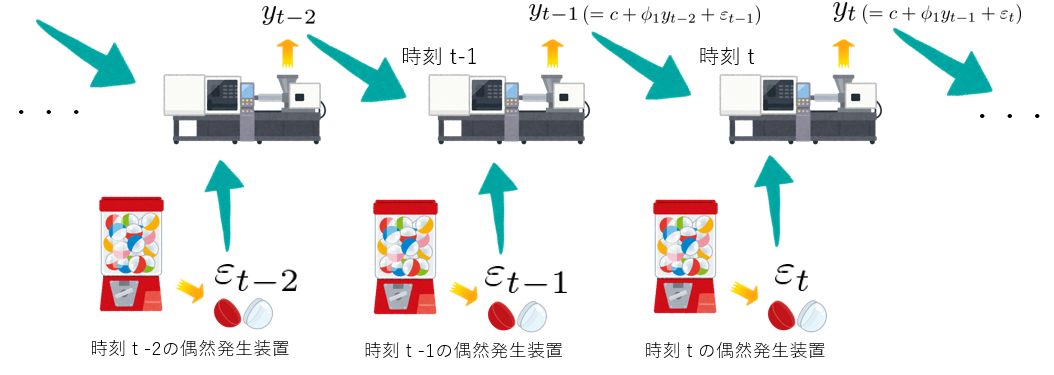
イメージ図を見てもらうと分かるのですが、偶然性を表している数値 \(\varepsilon_t\) も「横並びのガチャガチャマシン」から吐き出されているので、この横並びのガチャガチャ自体も時系列モデルと言えます。
ARモデルで使われている、この「横並びガチャガチャマシン」のことをホワイトノイズといいます。上記の数式内の
$$ \varepsilon_t \sim \textrm{W.N.}(\sigma^2) $$
の部分は、「ランダム項 \(\varepsilon_t \) はホワイトノイズから吐き出される値だよ!」ということを表しています。
じゃあ、ホワイトノイズはどんなマシンなんでしょうか?お硬く、定義を書くと、こうだ!
- 性質①:\( \textrm{E}[\varepsilon_t] = 0,~~~\forall t \)
- 性質②:\( \textrm{Var}[\varepsilon_t] = \sigma^2,~~~\forall t \)
- 性質③:\( \textrm{Cov}[\varepsilon_t, \varepsilon_{t-k}] = 0~~~\forall t,~k\)
を満たす確率過程のことを指します。はい、翻訳しますね。
「横並びのマシンがどれも0を中心に (←性質①) 散らばり具合 \(\sigma^2\) で (←性質②) 数値を吐き出して、なおかつ、どのマシンも他のマシンが吐き出した値の影響を受けない (←性質③) マシンの並び」です。
要は、同じ型のマシンが互いの干渉を受けずに横並びに置いてあるだけの状態です。(本当は、マシン同士が全く関係していないというわけでないのですが、とりあえずは関係ないと考えてもらって差し支えないです。本当に全く影響し合わない同じ型のマシンの並びを独立同分布といいます。)
2. 定常性とエルゴード性
\( | \phi_1 | < 1 \) のとき、AR(1) モデルの平均 \( \mu_t \)、分散 \( \sigma_t^2 \)、自己共分散 \( \gamma_{k, t} \)、自己相関係数 \( \rho_{k, t} \) は以下のようになります。
$$
\begin{align*}
\mu_t &= \frac{1}{1 – \phi_1} c \\
\sigma_t^2 &= \frac{\sigma^2}{1 – \phi_1^2} \\
\gamma_{k, t} &= \phi_1^k \gamma_0 \\
\rho_{k, t} &= \phi_1^k
\end{align*}
$$
着目すべきは、平均・分散が時刻 \( t \) に依らず、自己共分散と自己相関係数は時間差 \( k \) だけで決まるという性質です。このような性質を (弱) 定常性と呼び、(弱) 定常性を持つ確率過程を (弱) 定常過程と呼びます。
さらに、ラグ \( k \) が大きくなるにつれて自己共分散 \( \gamma_k \) が十分に早く \( 0 \) に収束するならば、定常過程の時間平均 (観測列の平均) \( \frac{1}{T} \sum_{t=1}^{T} y_t \) が空間平均 \( \mu_t = \textrm{E}(y_t) \) に確率収束します。 この性質をエルゴード性と呼びます。
エルゴード性のおかげで、空間平均を (観測値の) 時間平均で推定できることが保証され、それによって切片 \( c \) や自己回帰係数 \( \phi_1 \) の推定が可能になります。観測値の時間平均を \( \hat{\mu} \) で表せば、切片と自己回帰係数の推定量 \( \hat{c}、 ~\hat{\phi}_1 \) は
$$
\begin{align*}
\hat{\phi}_1 &= \frac{ \sum_{t=2}^T ( y_t – \hat{\mu} ) ( y_{t-1} – \hat{\mu} ) }{ \sum_{t=1}^T ( y_t – \hat{\mu} )^2 } \\
\hat{c} &= ( 1 – \hat{\phi}_1 ) \hat{\mu}
\end{align*}
$$
と表すことができます。(この推定量は厳密には最小二乗法により導出されます。最尤法やYule-Walker法など、他の方法で構築される推定量もあります。推定量の構築などの理論的は難所には踏み込まない..!)
難しい言葉をポンポン並べてしまいましたので、もう少し噛み砕いてイメージを説明します。
まず、定常性とエルゴード性の条件を課す背景には、時系列データの特殊性があります。通常のデータは、ある確率変数について複数の実現値があるため、それらを用いて平均や分散などのパラメータを推定することができますが、時系列データの場合、1つの時刻に対して1つの実現値しか存在しません。すなわち、昨日の気温を生成する確率変数の平均や分散を推測したいからといって、昨日の気温を何度も観測することはタイムリープができたりしない限り原理的に不可能ということです。あくまで実現値は1つしか得られません。1つの確率変数に対して、1つの実現値しかないため、そのままでは分散ですら推定できなくなります。そこで、過去100日分に得られた気温データを、今日の気温のパラメータ推定に利用できることを保証してくれる性質が、定常性とエルゴード性というわけです。
3. AR(p)モデル
今までは、1時刻前の自分自身を説明変数としてきましたが、より一般に \( p \) 時刻前までの自分自身を説明変数としたARモデルを \( p \) 次のARモデルと呼び、AR(p)モデルと表します。
$$
y_t = c + \sum_{i=1}^p \phi_i y_{t-i} + \varepsilon_t,~~~~\varepsilon_t \sim \textrm{W.N.}(\sigma^2)
$$
性質は次のようになります。
$$
\begin{align*}
\mu &= \textrm{E}[y_t] = \frac{c}{1-\sum_{i=1}^p \phi_i} \\
\gamma_0 &= \textrm{Var}[y_t] = \frac{\sigma^2}{1-\sum_{i=1}^p \phi_i \rho_i} \\
\gamma_k &= \sum_{I=1}^{p} \phi_i \gamma_{k-i},~~~k \ge 1 \\
\rho_k &= \sum_{I=1}^{p} \phi_i \rho_{k-i},~~~k \ge 1 \\
\end{align*}
$$
4. pythonによるARモデルの実装
今回は、農林水産省が発表している牛乳生産量のデータを取得し、このデータをARモデルを用いて分析していきます。(サウナ上がりのコーヒー牛乳が美味しかったので、このデータセットにしました。)
1985-01-31 591919
1985-02-28 546518
1985-03-31 622400
1985-04-30 628679
1985-05-31 661391
...
2018-08-31 606470
2018-09-30 560308
2018-10-31 596228
2018-11-30 579820
2018-12-31 609506
Freq: M, Length: 408, dtype: int64
ARモデルは定常過程にしか適用できないため、まずは時系列データが定常過程に従うかどうかを検定する必要があります。この場合は、ADF検定 (augmented Dicker-Fuller test) をすることで定常過程かどうかの確認が行えます。本記事では、ADF検定の詳細は省きますが、検定の結果、1次差分系列 \( \Delta y_t ~\small{(= y_t – y_{t-1})} \) が定常過程であることが分かりました。
次に、ARモデルの次数を決定する必要があります。一般に説明変数が多ければ多いほど、モデルは観測データにぴったりとフィットしますが、その一方で過剰適合の問題が発生します。過剰適合が起こると、今度は予測精度が落ちます。つまるところ、”たまたま得られただけの”観測値を頑張って説明しようとしすぎるあまり、新しく得られるデータの予測がおざなりになるということです。
ここでは、赤池情報量基準 (AIC: Akaike information criterion) という量を比較して次数を決定します。AICは、モデルの適合度による加点要素とパラメータの多さによる減点要素を同時に加味した量であり、AICの値が小さいほど適切なモデルと言えます。ここでは、詳しい理論の説明は省略します。
ここでは、pythonの統計解析用ライブラリStatsModelsを使用して、分析を行います。
# statsmodelsのtsa(time series analysis)モジュールから ar_modelクラスをインポート
from statsmodels.tsa import ar_model
# 農林水産省のサイトからデータを取得して、いい感じに加工した原系列を y に格納しています。
# 1次差分系列:y_diff
y_diff = y.diff().dropna()
# y_diff_train:2016年までのデータを訓練データとする
# y_diff_test:2017年以降のデータをテストデータとする
y_diff_train = y_diff[:'2016']
y_diff_test = y_diff['2017':]
# ARモデルの構築
model = ar_model.AR(y_diff)
# モデルのフィッティング
# maxlag(=20)までの次数の中でAICを最小にする次数を自動選択してくれる
results = model.fit(maxlag=20, ic='aic')results.k_ar で選択された次数を確認できます。ここでは、次数13が選択されました。
さて、構築されたAR(13)モデルの良し悪しを判断する場合、残差 (residual error) \( \varepsilon_t \) がホワイトノイズかどうかが重要です。残差は実際値とモデル予測値の誤差であり、もしある時系列モデルが時系列データの自己相関性質をうまく説明できたら、残差の自己相関は無相関になるはすです。
時系列がホワイトノイズの場合、データ数が \( n \) のとき、自己相関係数の標準偏差は \( \frac{1}{\sqrt{n}} \) となるので、残差の自己相関係数が \( \pm \frac{1.96}{\sqrt{n}} \) の95%信頼区間に収まっていれば、良いモデルが構築できていると言えます。
では、今回の結果の残差を確認しましょう。
from statsmodels.graphics import tsaplots
# 残差
resid = results.resid
# 残差の(偏)自己相関係数を次数50まで描画
tsaplots.plot_pacf(resid, lags=50)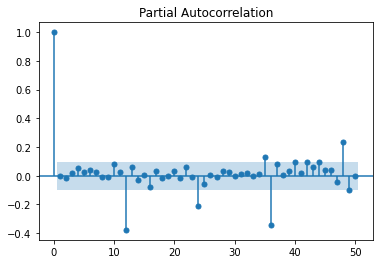
水色部分は、95%信頼区間を表しています。ラグ12の偏自己相関は信頼区間から外れているので無相関ではなさそうです。このモデルが1次階差系列にある12ヵ月の循環成分を十分に表現できているとは言えるでしょう。
最後に、このモデルの予測とテストデータ (2017年と2018年) を重ねて、いい感じで予測できているのか確認してみます。青線が実際の値で、オレンジ色の点線が予測です。
# 予測
y_diff_pred = results.predict('2017','2018')
# 予測をテストデータに重ねて描画
plt.plot(y_diff_test)
plt.plot(y_diff_pred, '--')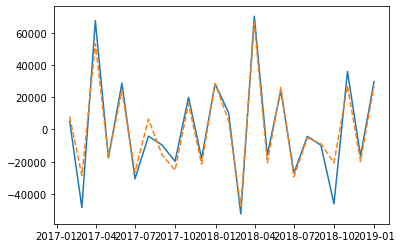
大まかに12ヵ月の周期を予測ができていそうですが、残差の自己相関で確認したように、周期性の表現が十二分とは言えないようです。
5. まとめ
今回はARモデルの性質を具体例に挙げながら、定常性やエルゴード性といった重要な時系列モデルの性質について説明しました。また後半では、実データを分析しながら、時系列解析における重要なプロセス (定常性の検定、AICによる次数決定、残差の自己相関によるモデルの良し悪しの判断….etc) を説明しました。次回は、MAモデル、そして、ARモデルとMAモデルをミックスしたARMAモデルを説明する予定です。
Comments are closed