1. はじめに

『 賭博破戒録カイジ 』という作品の中で、地下チンチロリンという賭け事が登場します。その賭けの中で主人公であるカイジは、大槻班長という人心掌握術に長けたタヌキにイカサマをしかけられてしまいます。そのイカサマに使用された不正なサイコロが、かの有名な「四五六賽」、４・５・６の面しか出ないという代物です。

主人公カイジは、類い稀な洞察力を駆使して、それまでの出目の記録からイカサマサイコロの不正を暴きました。凡人の私には気づけそうもないので、数学の力をお借りして、大槻班長のイカサマを暴いていこうと思います。

2. 隠れマルコフモデル：Hidden Markov model

まずは、この大槻班長のイカサマ行動を隠れマルコフモデル (Hidden Markov model: HMM) というモデルを使って、モデリングしていきます。

隠れマルコフモデルは、時系列データのパターン認識に使用されることが多く、音声認識・形態素分析・バイオインフォマティクス・金融データの分析などの多くの分野で応用されています。

早速ですが、モデリングしていきます。

\( t \) 回目のロール ( = サイコロを振ること ) で大槻班長が使用しているサイコロの種類を \( x_t \) と表すことにします。 作中では、通常のサイコロと四五六賽の２種類のサイコロが使用されていましたが、ここでは一般化して、\( M \) 種類のサイコロ \(s_1,…,s_M \) が使用されているとします。また、 \( t \) 回目のロールの出目を \( y_t \) と表すことにします。サイコロは \(6\) 面ですが、これも一般化して、\( N \) 面サイコロ、つまり出目の種類が \( o_1, …, o_N \) であるとします。

• \( t \) 回目に大槻班長が使用しているサイコロの種類：\( x_t \)
• \( t \) 回目の出目：\( y_t \)
• サイコロの種類：\( s_1,…,s_M\)
• サイコロの面の種類：\( o_1,…,o_N \)

記述を簡便にするために、\( x_{t|t^\prime} := \{x_t,…,x_{t^\prime}\},~ y_{t|t^\prime} := \{y_t,…,y_{t^\prime}\} \) という記法を使用します。

ここで大槻班長はマルコフモデルに従って、サイコロを選択するとします。すなわち、一回前に使用されたサイコロの種類によって、次のサイコロの種類が確率的に決まるという仮定を置きます。(かなり乱暴な仮定ですが、許してね！)

\(t-1\) 回目にサイコロ\( s_i \)に使用された下で、\( t\) 回目にサイコロ\(s_j\) が使用される確率を

$$ a(s_i, s_j) := P(x_t = s_j | x_{t-1} = s_i)$$

と表します。\( a(s_i, s_j) \) は状態 \(s_i\) から状態\( s_j \) への遷移確率 (transition probability) といい、\( a(s_i, s_j) \) を \( (i,j)\) 成分にもつ行列 \(A\) を遷移行列 (transition matrix) といいます。

\( t\) 回目にサイコロ\(s_j\) が使用された下で、出目が \( o_k\) となる確率を

$$ b(s_j, o_k) := P(y_t = o_k | x_t = s_j) $$

と表します。これは出力確率 (emission probability)と呼ばれ、これを \( (j,k)\) 成分にもつ行列 \( B\) を出力行列 (emission matrix)と呼びます。例えば、通常のサイコロを \( s_1 \) とすると、

$$ b(s_1, o_1) = b(s_1, o_2) = b(s_1, o_3) = b(s_1, o_4) = b(s_1, o_5) = b(s_1, o_6) = \frac{1}{6}$$

となり、四五六賽を \( s_2 \) とすると

$$ b(s_1, o_1) = b(s_1, o_2) = b(s_1, o_3) = 0,~~b(s_1, o_4) = b(s_1, o_5) = b(s_1, o_6) = \frac{1}{3}$$

となります。しがたって、出力確率行列は

$$B = \begin{bmatrix}1/6& 1/6& 1/6& 1/6& 1/6& 1/6\\ 0&0&0&1/3&1/3&1/3\end{bmatrix}$$

となります。

\( a(s_i, s_j) , b(s_j, o_k) \) は適宜、\( a_{ij}, b_{jk} \) と略記するので注意してください。

最後に、大槻班長が \(1 \) 回目にサイコロ \( s_i \) を使用する確率を \(\pi_i \) で表し、これらを要素にもつベクトル \( \boldsymbol{\pi} = (\pi_1,…,\pi_M) \) を初期状態確率ベクトル (initial probability vector) と呼びます。

いま規定した遷移行列 \(A\)・出力行列 \( B \)・初期状態確率ベクトル \( \boldsymbol{\pi} \) はHMMを規定するパラメータなので、これらの組を \(\boldsymbol{\theta}= (A, B, \boldsymbol{\pi}) \) と表し、HMMパラメータ ( もしくは単にパラメータ ) と呼ぶことにします。

我々からは、大槻班長がどのサイコロを使用しているか知る術はありません。このように、”マルコフ過程” に従っているサイコロの状態 \( x_i \) が観測者 (= 賭けの相手) から “隠れている” ことが “隠れマルコフ” モデルという名の由来です。

また、隠れマルコフモデルは、状態変数が離散値である状態空間モデルと言えます。観測値は離散・連続値のどちらでも構いませんが、今回は観測値側も離散値である場合について議論を進めていきます。

【状態空間モデル】カルマンフィルタを Pythonで実装してみた

2.1. 学習問題：Learning problem

いま我々は、大槻班長が一番初めにどのサイコロを使う傾向があったのか ( = 初期状態確率ベクトル \( \boldsymbol{\pi} \) ) 、サイコロの使い分けにどんな傾向があったのか ( = 遷移行列 \( A \) ) 、そして各サイコロはどのような目が出やすかったのか ( = 出力行列 \( B \) ) 、何も知りません。いつイカサマが行われていたか調べるためには、出目の記録を基にして、大槻班長の行動パターン ( \(A, \boldsymbol{\pi} \) ) や各サイコロの性質 ( \(B\) ) を推測することから始めなければなりません。すなわち、得られている観測結果 \(y_{1:T}\) から未知のパラメータ \( \boldsymbol{\theta} = (A,B,\boldsymbol{\pi}) \) を推測する必要があるということです。このような問題を学習問題と呼びます。

さて、観測できない変数 ( = 潜在変数 ) を含むようなモデルの未知パラメータを求めるには、EMアルゴリズムがよく使われます。今回は、EMアルゴリズムのHMMバージョンであるBaum-Welchアルゴリズムを用いて、未知のパラメータ \( \boldsymbol{\theta} = (A,B,\boldsymbol{\pi}) \) を推定します。(EMアルゴリズムの概要やBaum-Welchアルゴリズムの導出は割愛します。)

---

■ Baum-Welch アルゴリズム

1. 初期化
   　パラメータ \( A, B, \boldsymbol{\pi} \) に適当な初期値を設定
2. 収束するまで以下を繰り返す
   1. Eステップ：下記の値を計算する
      \(~~~ \gamma_t(j) := P(x_t = s_j | y_{1:T}),~~~\forall t, j \)
      \(~~~ \xi_t(i, j) := P(x_t = s_i, x_t = s_j | y_{1:T}),~~~\forall t, i, j \)
   2. Mステップ：下記の値を計算する
      \( ~~~\hat{a}_{i,j} := \sum_{t=1}^{T-1} \xi_t(i, j) \bigl/ \sum_{t=1}^{T-1} \gamma_t(i) \)
      \( ~~~\hat{b}_{j,k} := \sum_{t=1}^{T} \delta(y_t, o_k) \gamma_t(j) \bigl/ \sum_{t=1}^{T} \gamma_t(j) \)
      \(~~~\hat{\pi}_i := \gamma_1(i) \)
   3. パラメータ更新
      \(~~~a_{i,j} \leftarrow \hat{a}_{i,j}, ~~b_{j,k}\leftarrow \hat{b}_{j,k},~~ \pi_i\leftarrow \hat{\pi}_i\)
      

---

このアルゴリズム通り計算していけば、パラメータの推定値が得られます。しかし、Eステップで求める必要がある \( \gamma_t(j), \xi_t(i,j) \) が解析的に表現されていないため、このままでは計算できず不完全です。

\( \gamma_t(j), \xi_t(i,j) \) を解析的に計算するために必要な２つの確率を定めます。

• 前向き確率：\( \alpha_t(j) := P(x_t = s_j , y_{1:t}) \)
• 後ろ向き確率：\( \beta_t(j) := P(y_{t+1:T}|x_t = s_j) \)

\( \gamma_t(j), \xi_t(i,j) \) を式変形すると、今ほど定義した前向き確率と後ろ向き確率 (それと遷移確率、出力確率) で表現することができます。

$$
\begin{align}
\gamma_t(j) &= P(x_t=s_j | y_{1:T}) \\
&= \frac{P(x_t = s_j, y_{1:T})}{P(y_{1:T})} \\
&= \frac{P(x_t = s_j, y_{1:t}) P(y_{t+1:T} | x_t=s_j)}{\sum_{i=1}^M P(x_T=s_i, y_{1:T})} \\
&= \frac{\alpha_t(j) \beta_t(j)}{\sum_{i=1}^M \alpha_T(i)} \\
\\
\xi_t(i,j) &= P(x_t = s_i, x_{t+1} = s_j | y_{1:T}) \\
&= \frac{P(x_t = s_i, x_{t+1}=s_j ,y_{1:T})}{P(y_{1:T})} \\
&= \frac{P(x_t = s_i, y_{1:t}) P( x_{t+1}=s_j | x_t=s_i) P(y_{t+1} | x_{t+1}=s_j) P(y_{t+2:T} | x_{t+1}=s_j) }{\sum_{i=1}^M P(x_T=s_i, y_{1:T})} \\
&= \frac{\alpha_t(i) a_{ij} b(s_j, y_{t+1})\beta_{t+1}(j)}{\sum_{i=1}^M \alpha_T(i)} \\
\end{align}
$$

ということで、天下り的ではありましたが、\( \gamma_t(j), \xi_t(i,j) \) を得るには、前向き確率と後ろ向き確率が求めればよいことが分かりました。この前向き確率と後ろ向き確率を計算するアルゴリズムをそれぞれ Forwardアルゴリズム、Backwardアルゴリズム といいます。そのため、Baum-Welchアルゴリズムは別名 Forward-Backwardアルゴリズム とも呼ばれます。

---

■ Forward アルゴリズム

1. 初期化
   \(~~~ \alpha_1(i) = \pi_i b(s_i, y_1),~~~\forall i =1,…,M \)
2. 反復：\(t=2 \) to \( T \)
   \(~~~ \alpha_t(j) = \Bigl(\sum_{i=1}^M a_{ij}\alpha_{t-1}(i)\Bigl)b(s_j, y_t),~~~\forall j =1,…,M \)

---

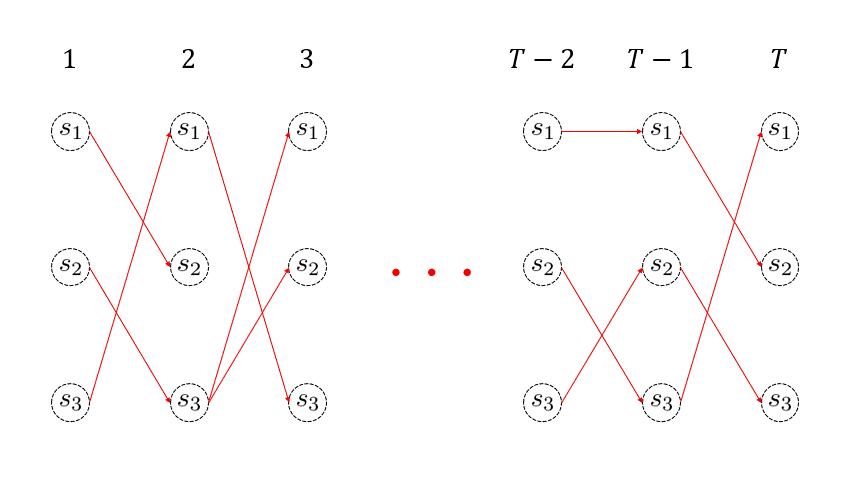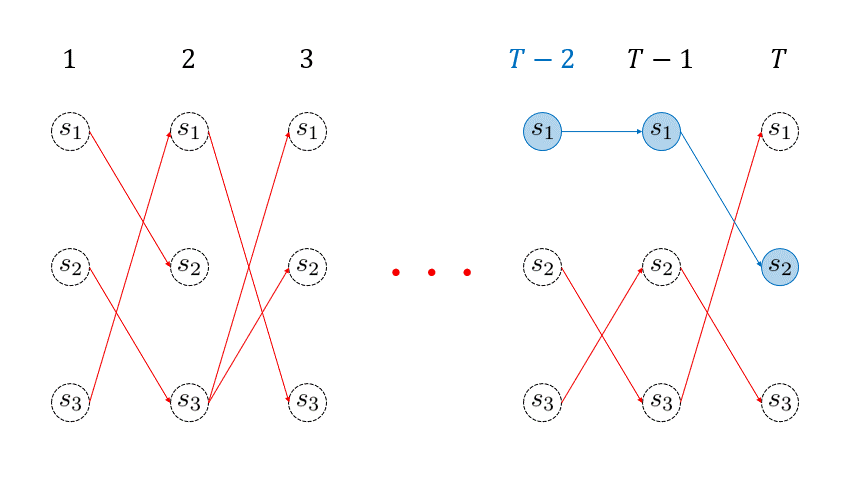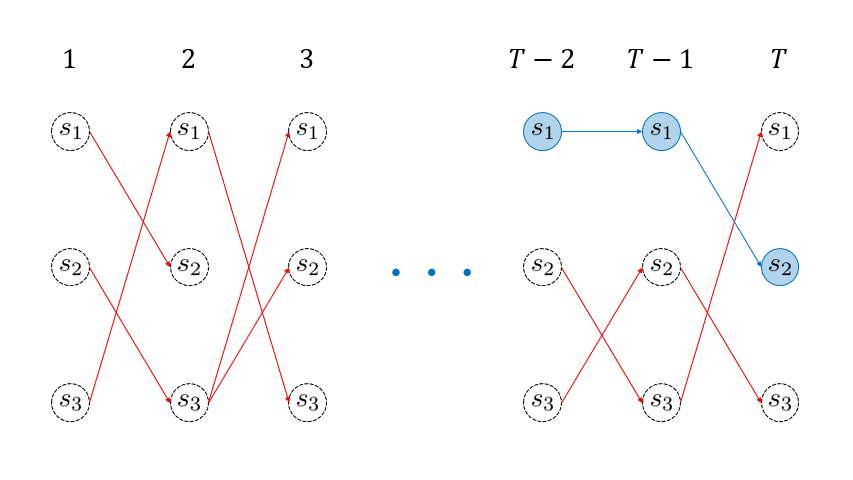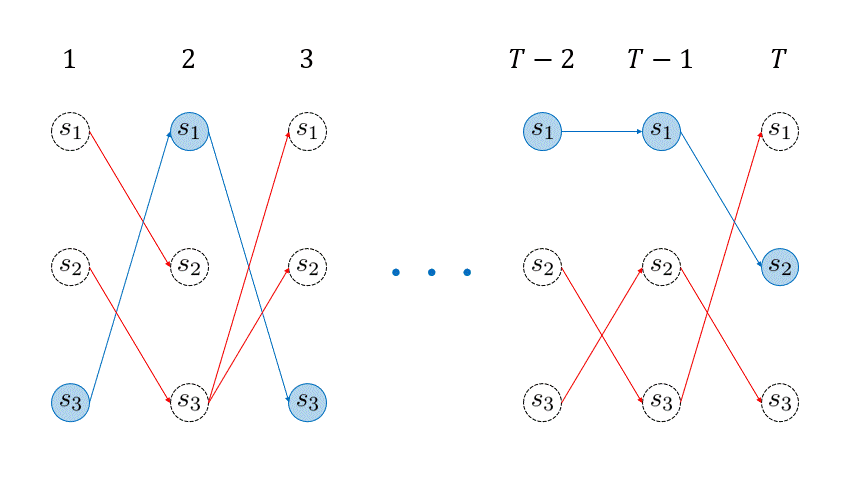
反復処理で用いられる漸化式の導出は記しませんが、下図のトレリスダイアグラム ( = 状態の遷移の様子を時間を追って見やすくしたもの ) から直観的理解が得られると思います。

---

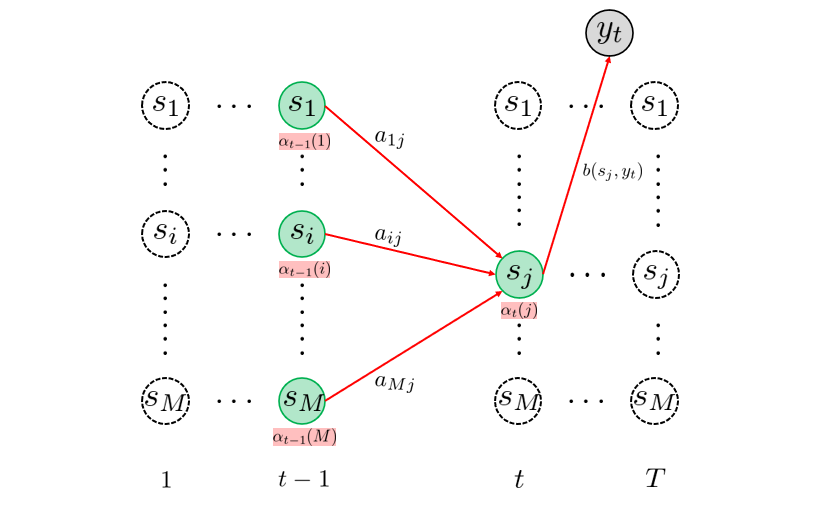
■ Backward アルゴリズム

1. 初期化
   \(~~~ \beta_T(i) = 1,~~~\forall i = 1,….,M \)
2. 反復：\(t=T-1 \) to \( 1 \)
   \(~~~ \beta_t(i) = \sum_{j=1}^M a_{ij}\beta_{t+1}(j)b(s_j, y_{t+1}),~~~\forall i =1,…,M \)
   

---

Backwardアルゴリズムも反復処理で用いられる漸化式部分も先程と同じように、トレリスダイアグラムで直観的に理解できると思います。トレリスダイアグラムを見比べると一目瞭然ですが、前向き確率は時間について、”前向き” に計算されていくのに対して、後ろ向き確率は ”後ろ向き” に計算されていきます。これが名前の由来です。

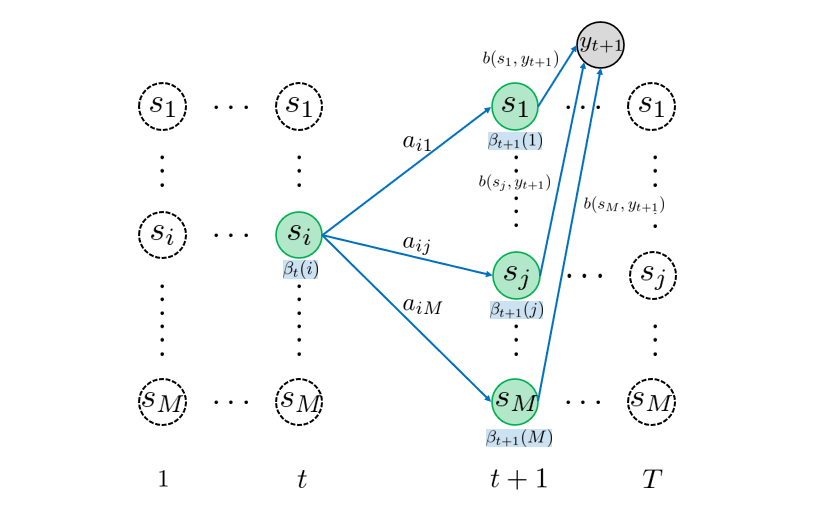
それでは、Baum-Welchアルゴリズムの不完全だった部分を修正したものを記していきます。

---

■ Baum-Welch アルゴリズム

1. 初期化
   　パラメータ \( A, B, \boldsymbol{\pi} \) に適当な初期値を設定
2. 収束するまで以下を繰り返す
   1. Eステップ：
      1. Forward アルゴリズム：\( \alpha_t(j),~~~\forall t, j \)　を計算
      2. Backward アルゴリズム：\( \beta_t(j),~~~\forall t, j \)　を計算
      3. 下記の値を計算する
         \(~~~ \gamma_t(j) :=\alpha_t(j) \beta_t(j) \bigl/ \sum_{i=1}^M \alpha_T(i) ,~~~\forall t, j \)
         \(~~~ \xi_t(i, j) := \alpha_t(i) a_{ij} b(s_j, y_{t+1}) \beta_{t+1}(j) \bigl / \sum_{i=1}^M \alpha_T(i),~~~\forall t, i, j \)
   2. Mステップ：下記の値を計算する
      \( ~~~\hat{a}_{i,j} := \sum_{t=1}^{T-1} \xi_t(i, j) \bigl/ \sum_{t=1}^{T-1} \gamma_t(i) \)
      \( ~~~\hat{b}_{j,k} := \sum_{t=1}^{T} \delta(y_t, o_k) \gamma_t(j) \bigl/ \sum_{t=1}^{T} \gamma_t(j) \)
      \(~~~\hat{\pi}_i := \gamma_1(i) \)
   3. パラメータ更新
      \(~~~a_{i,j} \leftarrow \hat{a}_{i,j}, ~~b_{j,k}\leftarrow \hat{b}_{j,k},~~ \pi_i\leftarrow \hat{\pi}_i\)
      

---

2.2. 評価問題：Evaluation problem

Forwardアルゴリズム と Backwardアルゴリズム に関連した、補足を入れておきます。

現象に対するモデルの説明力を “評価” するには、AIC (赤池情報量基準) やBIC (ベイズ情報量基準) などの評価基準を用います。どの評価基準を使用するにしても、大前提として尤度が得られている必要があります。したがって、「パラメータが与えられた下で、尤度を求める問題」は 評価問題 と呼ばれます。上述した２つのアルゴリズムは前向き確率と後ろ向き確率を求めるための手法として説明してきましたが、他方でこの評価問題を解決するための手法であるとも言えるわけです。実際、前向き確率を用いて、

$$
\begin{align*}
P(y_{1:T}) &= \sum_{i=1}^M \alpha_T(i) \\
\end{align*}
$$

もしくは、後ろ向き確率を用いて、

$$ P(y_{1:T}) = \sum_{i=1}^M \pi_i b(s_i, y_1) \beta_1(i) $$

を計算することで尤度を求められます。

2.3. 復号化問題：Decoding problem

さて、我々はBaum-Welchアルゴリズムを用いて、

• 大槻班長が一番初めに選ぶサイコロの傾向 ( = 初期状態確率ベクトル \( \boldsymbol{\pi} \) )
• 大槻班長がサイコロを使い分ける傾向 ( = 遷移行列 \( A \) )
• 各サイコロの出目の傾向 ( = 出力行列 \( B \) )

を推定することができました。これらの情報と出目の結果を基に、いつイカサマが行われていたのかを暴いていきます。より具体的にいうと、「大槻班長が取り得たサイコロの選択順序のうち、最も可能性が高い順序を見つけ出す」ということです。

すなわち、観測結果 \( y_{1:T} \) とパラメータ \( \boldsymbol{\theta} = ( A, B, \boldsymbol{\pi}) \) が与えられた下で、確率 \( P(y_{1:T} | x_{1:T} ) \) を最大にするようなパス \(x_{1:T} \) を求める問題と言えます。この問題は復号化問題といい、復号化問題を効率的に解くアルゴリズムとして、Viterbiアルゴリズム というものがあります。

Viterbiアルゴリズムではまず、「観測 \( y_{1:t}\) が得られ、かつ時刻 \( t \) に状態 \( s_i \) に遷移する最も高い確率 」

$$
\omega_t(i) = \underset{x_{1:t-1}}{\max} p(x_{1:t-1}, x_t = s_i, y_{1:t})
$$

を定義します。これは以下の式を用いて、動的計画法の要領で再帰的に求めることができます。

$$ \omega_{t+1}(j) = \underset{i=1,…,M}{\max}\Bigl(\omega_t(i)a_{ij}\Bigl) \cdot b(s_j, y_{t+1}) $$

下のアニメーションの赤線が引かれていく様子が、各回の各状態 \( \omega_{t}(j) \) を再帰的に求めていくイメージを表しています。 このように、各回の各状態に対して、そこに遷移する最大確率パス (赤線) を生存者パス ( survivor path ) と言います。例えば、時刻 \(t=3 \) に状態 \(s_3\) に遷移する生存者パスは、\( \underset{(t=1)}{s_3} \rightarrow \underset{(t=2)} {s_1} \rightarrow \underset{(t=3)} {s_3} \) となります。

また、どの経路を通ってきたかを記憶しておくために、各生存者パスのゴールの一つ前の状態を保存しておきます。すなわち、

$$ \sigma_{t+1}(j) = \underset{i=1,…,M}{\arg\max} \Bigl( \omega_t(i)a_{ij} \Bigl) $$

を取得しておくということです。例えば、下のアニメーションの \( t=2\) 回目において、状態 \(s_1\) に遷移する生存者パスのゴールの一つ前の状態 ( \(t=1\) 回目の状態 ) は \(s_3 \) です。しがたって、\( \sigma_2(1) = 3 \) となります。

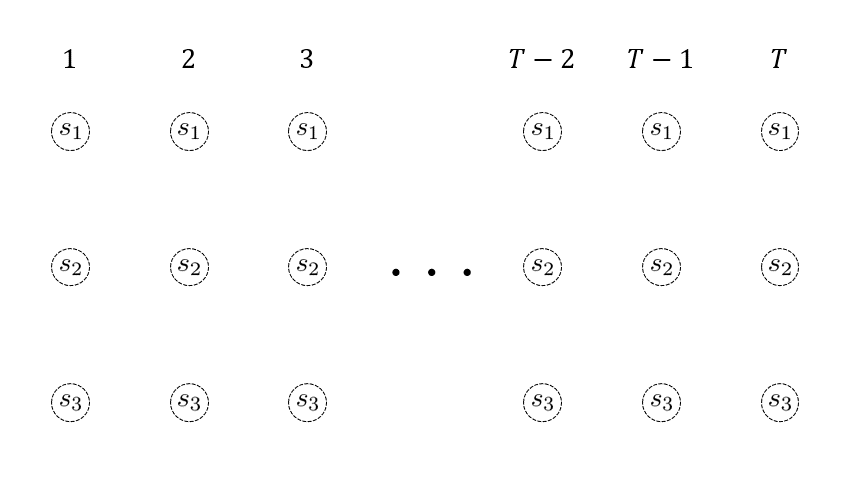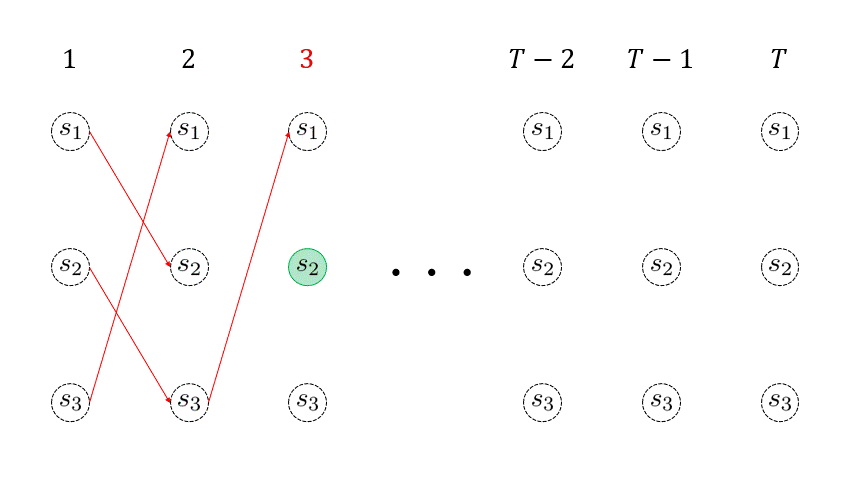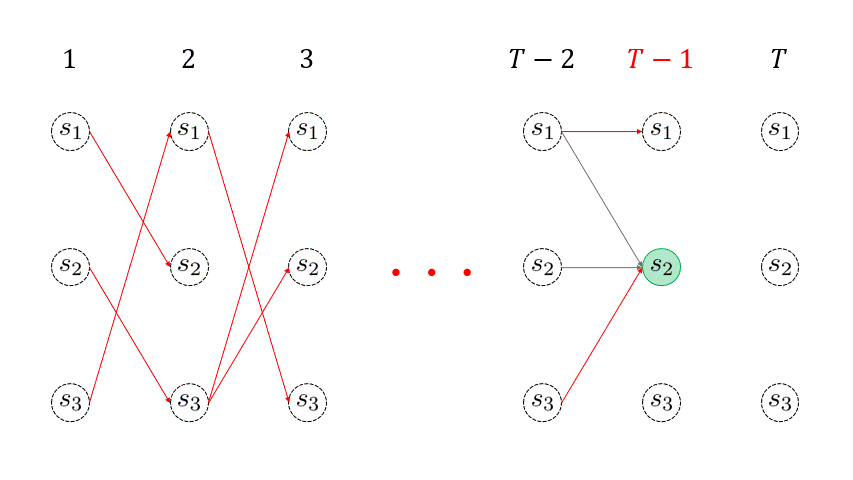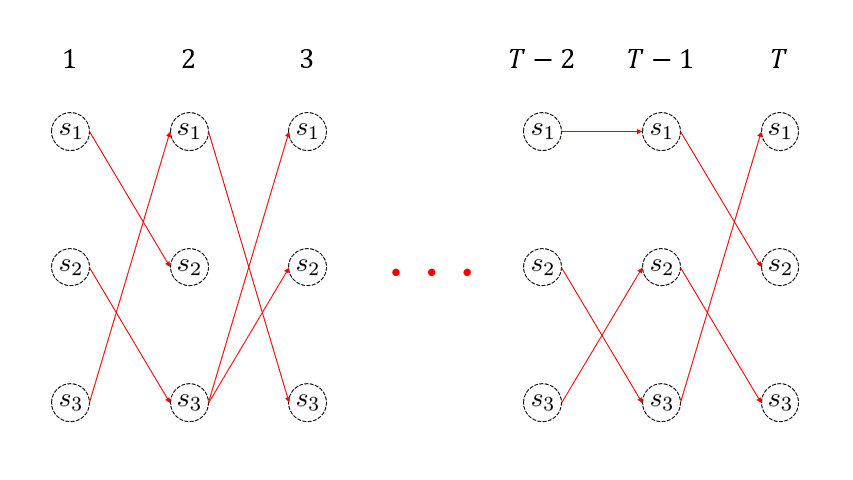
\( T\) 回目までの再帰処理を終えたら、

$$ q_T = \underset{i=1,…,M}{\arg\max} \Bigl( \omega_T(i) \Bigl) $$

を求めます。つまり、\( T \) 回目に最も尤もらしかった状態を取得するわけです。そして、\(T\) 回目における最も尤もらしい状態が分かれば、その生存者パスが最も尤もらしいパスとなるわけです。さきほど、生存者パスの直前状態の情報を \( \sigma_{t}(j) \) に格納しておいたので、

$$ q_t = \sigma_{t+1}(q_{t+1}) $$

を再帰的に用いて、目的のパスを復元することができます。このように得られた最も尤もらしい経路は Viterbiパス (Viterbi path) と呼ばれます。こちらの処理もイメージをアニメーションにしました。

3. Pythonによる実装

ライブラリ

import numpy as np

Forwardアルゴリズム

def forward(observations,
            transition_matrix,
            emission_matrix,
            initial_distribution):
    n_timesteps = observations.shape[0]
    n_states = transition_matrix.shape[0]
    forward_prob = np.zeros((n_timesteps, n_states))
    
    forward_prob[0, :] = initial_distribution * emission_matrix[:, observations[0]]
    
    for t in range(1, n_timesteps):
        for j in range(n_states):
            forward_prob[t, j] = (
                forward_prob[t-1]
                @ transition_matrix[:, j]
                * emission_matrix[j, observations[t]]
            )
            
    return forward_prob

Backwardアルゴリズム

def backward(observations,
             transition_matrix,
             emission_matrix):
    n_timesteps = observations.shape[0]
    n_states = transition_matrix.shape[0]
    backward_prob = np.zeros((n_timesteps, n_states))
    
    backward_prob[n_timesteps-1] = np.ones((n_states))
    
    for t in reversed(range(0, n_timesteps-1)):
        for j in range(n_states):
            backward_prob[t, j] = (
                (backward_prob[t+1]
                 * emission_matrix[:, observations[t+1]]
                ) @ transition_matrix[j, :]
            )
            
    return backward_prob

Baum-Welchアルゴリズム

def baum_welch(observations,
               transition_matrix,
               emission_matrix,
               initial_distribution,
               n_iter=100):
    n_timesteps = observations.shape[0]
    n_states = transition_matrix.shape[0]
    
    for n in range(n_iter):
        # E-step
        forward_prob = forward(
            observations,
            transition_matrix,
            emission_matrix,
            initial_distribution
        )
        backward_prob = backward(
            observations,
            transition_matrix,
            emission_matrix
        )
        
        xi = np.zeros((n_states, n_states, n_timesteps-1))
        
        for t in range(n_timesteps-1):
            xi_denominator = (
                forward_prob[t, :].T
                @ transition_matrix
                * emission_matrix[:, observations[t+1]].T
                @ backward_prob[t+1, :]
            )
            for i in range(n_states):
                xi_numerator = (
                    forward_prob[t, i]
                    * transition_matrix[i, :]
                    * emission_matrix[:, observations[t+1]].T
                    * backward_prob[t+1, :].T
                )
                xi[i, :, t] = xi_numerator / xi_denominator
                
        gamma = np.sum(xi, axis=1)
        
        # M-step
        transition_matrix = np.sum(xi, axis=2) / np.sum(gamma, axis=1).reshape((-1, 1))
    
        gamma = np.hstack((gamma, np.sum(xi[:, :, n_timesteps-2], axis=0).reshape((-1, 1))))
        n_symbols = emission_matrix.shape[1]
        denominator = np.sum(gamma, axis=1)
        
        for i in range(n_symbols):
            emission_matrix[:, i] = np.sum(gamma[:, observations == i], axis=1)
 
        emission_matrix = np.divide(emission_matrix, denominator.reshape((-1, 1)))
 
    return (transition_matrix, emission_matrix)

Viterbiアルゴリズム

def viterbi(observations,
            transition_matrix,
            emission_matrix,
            initial_distribution):
    n_timesteps = observations.shape[0]
    n_states = transition_matrix.shape[0]
    
    omega = np.zeros((n_timesteps, n_states))
    omega[0, :] = np.log(initial_distribution * emission_matrix[:, observations[0]])
 
    prev = np.zeros((n_timesteps-1, n_states))
 
    for t in range(1, n_timesteps):
        for j in range(n_states):
            prob = (
                omega[t-1] 
                + np.log(transition_matrix[:, j])
                + np.log(emission_matrix[j, observations[t]])
            )
            prev[t-1, j] = np.argmax(prob)
            omega[t, j] = np.max(prob)
 
    viterbi_path = np.zeros(n_timesteps)
    
    last_state = np.argmax(omega[n_timesteps-1, :])
    viterbi_path[n_timesteps-1] = last_state
    
    for t in reversed(range(0, n_timesteps-1)):
        viterbi_path[t] = prev[t, int(last_state)]
        last_state = prev[t, int(last_state)]
 
    return viterbi_path

4. 大槻班長を成敗してみた

真のパラメータを

• 遷移行列 \( A= \begin{bmatrix}0.99 & 0.01 \\ 0.05 & 0.95\end{bmatrix}\)
• 出力行列 \( B= \begin{bmatrix}1/6 & 1/6& 1/6& 1/6& 1/6& 1/6 \\ 0 & 0& 0& 1/3& 1/3& 1/3\end{bmatrix}\)
• 初期状態確率ベクトル \( \boldsymbol{\pi}= \begin{bmatrix}1\\0 \end{bmatrix}\)

として、サイコロを300回振り、状態遷移のパスと出目の観測値を得ました。下図は真の状態遷移の様子です。緑が通常のサイコロを使用していた期間、赤が四五六賽を使用していた期間です。

観測値を基に推定したViterbiパスが下図です。概ね的中させることができています。青線は、「四五六賽が使用されている」事後確率を表しています。

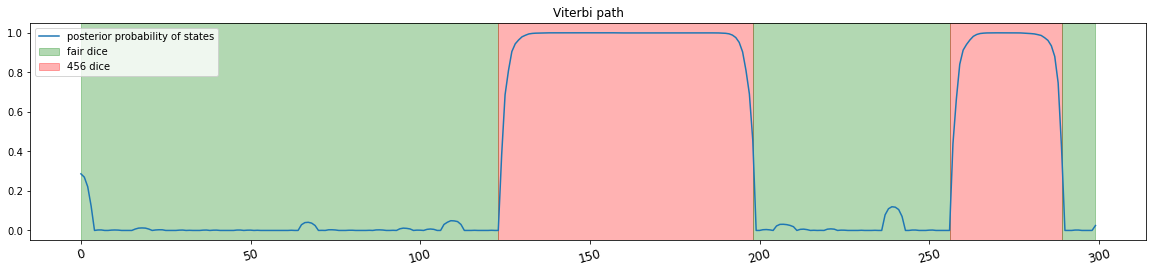
真の状態遷移とViterbiパスの結果が異なる区間だけを灰色で図示しました。