Prophetの概要
ProphetはFacebook社が開発した時系列解析ライブラリです.
Prophetでは, 時系列データ \(y(t)\) を3つの項の和としてモデリングします.
$$ y(t) = g(t) + s(t) + h(t) + \varepsilon_t$$
- \(g(t)\) : 成長関数(growth)→時間と共に単調に変動する項
- \(s(t)\) : 周期関数(seasonality)→周期的に繰り返される変動
- \(h(t)\) : 祝日効果(holiday)→イレギュラーなカレンダー上の日程が与える影響
- \(\varepsilon_t\) : 誤差項
上記のようなモデルは一般化加法モデルと呼ばれ, このモデルでは平滑化(スムージング)と呼ばれる関数型に依存しない自由な回帰を行います.
平滑化を用いて予測するということは, 自己回帰型モデル(ARIMA等)などの伝統的な時系列モデルとは考え方が根本的に異なります.
古典的な時系列モデルでは, 過去のデータと未来のデータの関係性をモデル化します. それに対して平滑化がするのは, データのグラフにいい感じな曲線を引いているだけ(要は回帰分析!)なので, 過去のデータと未来のデータの関係性などの情報はゴミ箱にポイしています.
その代わりに, Prophetモデルには様々なメリットがあります. 例えば, Prophetモデルでは欠損値を補完しなくても学習ができる点です.
伝統的な時系列モデルでは, 各時刻のデータの関係性を記述しています. 例として AR(1)モデルを考えてみます.
例) AR(1)モデル $$X_t = c + \varphi X_{t-1} + \varepsilon_t$$
上式を見てわかるように, AR(1)モデルでは1時点前の出力が次点のモデルを与えます. これは, ある1時点のデータが欠損すると, それより先の時点の計算ができなくなることを意味しています.したがって, 自己回帰モデル等の伝統的な時系列モデルでは, データの前処理として欠損値を何かしらの値で補完する必要があるのです.
一方で, Prophetモデルは通常の回帰モデルと同様に, 観測されたデータにいい感じに曲線を引くという手法ですから, ある時点のデータが欠けていようがお構いなしです. ( 例えば, 年齢と体重の関係を回帰分析する場合に, 22歳のときの身長を測り忘れていたとしても回帰分析できますよね?それと同じです.)
この他にも, たくさんのメリットがありますが, とにかく「楽に時系列分析できる」がモットーのモデルなようです.
インストール
pip install Prophet
# anacondaを使用している方は
conda install -c conda-forge fbprophet ※ 筆者はProphet使用中に KeyError: 'metric_file' というエラーを吐かれました. pystanのversionが古いことが原因ぽかったので, 下記を参考に pystanのversionをアップグレードしました. (ちなみに, Prophetの処理自体はpystanで書かれているようです)
https://github.com/facebook/prophet/issues/1670
ライブラリのインポート
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from fbprophet import Prophet
from pandas_datareader.data import DataReader
import datetime
データ取得&整形
pandasのDataReaderを使用して, 「Yahoo!ファイナンス」からトヨタの株価データを取得します.
start = datetime.date(2018,1,1)
end = datetime.date(2021,1,1)
data_train = DataReader('TM', 'yahoo', start, end)以下のような2018年1月から2020年12月のトヨタの株価データになっています.
| High | Low | Open | Close | Volume | Adj Close | |
|---|---|---|---|---|---|---|
| Date | ||||||
| 2018-01-02 | 128.429993 | 127.169998 | 127.430000 | 128.369995 | 83500 | 128.369995 |
| 2018-01-03 | 130.240005 | 128.559998 | 128.679993 | 130.130005 | 162200 | 130.130005 |
| 2018-01-04 | 132.160004 | 131.300003 | 131.309998 | 132.160004 | 161800 | 132.160004 |
| 2018-01-05 | 133.869995 | 133.080002 | 133.110001 | 133.860001 | 135300 | 133.860001 |
| 2018-01-08 | 134.789993 | 133.619995 | 133.979996 | 134.770004 | 131200 | 134.770004 |
| … | … | … | … | … | … | … |
| 2020-12-24 | 151.130005 | 150.179993 | 150.179993 | 150.470001 | 150200 | 150.470001 |
| 2020-12-28 | 153.419998 | 152.229996 | 153.100006 | 152.600006 | 215600 | 152.600006 |
| 2020-12-29 | 155.199997 | 152.899994 | 155.000000 | 153.339996 | 265100 | 153.339996 |
| 2020-12-30 | 155.210007 | 154.039993 | 154.509995 | 154.089996 | 193500 | 154.089996 |
| 2020-12-31 | 154.839996 | 153.970001 | 154.410004 | 154.570007 | 160000 | 154.570007 |
このデータのうち, 予測に利用するのは `Adj Close` カラムです. これは調整後終値という値です.
( 調整後終値とは? https://support.yahoo-net.jp/PccFinance/s/article/H000006678 )
「時刻を表す列は ds , 予測する値の列は y で表す」というProphetの仕様に合わせて, データを整形します.
data_train['ds'] = data_train.index
data_train = data_train.rename({'Adj Close':'y'}, axis=1)株価は対数をとるのが通例らしいので , y列に対数を被せます.
株価チャートは「線形グラフ」だけでなく「対数グラフ」でも見る習慣をつけよう【初心者必見】 https://www.35kara.com/2020/07/what-are-a-linear-graph-and-a-log-graph.html
data_train['y'] = np.log(data_train['y'])学習パート
model = Prophet()
model.fit(data_train)parameter
モデルには以下のパラメータが設定可能です。問題により適切なパラメータを設定することで精度が向上します。
- growth: トレンドを表す関数(線形かロジスティック曲線)
- changepoints: トレンドの変化点のリスト
- n_changepoints: トレンドの変化点の数
- changepoint_range: トレンドの変化点を推測する幅
- yearly_seasonality: 年単位の周期性を考慮するか
- weekly_seasonality: 週単位の周期性を考慮するか
- daily_seasonality: 日単位の周期性を考慮するか
- holidays: 休日
- seasonality_mode: 周期性の傾向
- seasonality_prior_scale: 周期性の強さを表すパラメータ
- holidays_prior_scale: 休日の強さを表すパラメータ
- changepoint_prior_scale: トレンドの変化点の強さを表すパラメータ
- mcmc_samples: MCMC法のサンプル数
- interval_width: 誤差の範囲の広さ
- uncertainty_samples: 誤差を推測するためのサンプル数
- stan_backend: バックエンドの指定
以下のようにパラメータの指定ができます。下記は全てデフォルト値になっています。
params = {'growth': 'linear',
'changepoints': None,
'n_changepoints': 25,
'changepoint_range': 0.8,
'yearly_seasonality': 'auto',
'weekly_seasonality': 'auto',
'daily_seasonality': 'auto',
'holidays': None,
'seasonality_mode': 'additive',
'seasonality_prior_scale': 10.0,
'holidays_prior_scale': 10.0,
'changepoint_prior_scale': 0.05,
'mcmc_samples': 0,
'interval_width': 0.80,
'uncertainty_samples': 1000,
'stan_backend': None}
model = Prophet(**params)予測パート
学習が完了したらテストデータで予測します。
make_future_dataframeで学習データの期間に予測したい期間を追加したDataFrameを作成します.
future = model.make_future_dataframe(
periods=365, # 予測する日数
freq = 'd' # 単位(d: 日)
)以下がfutureの中身です.
| ds | |
|---|---|
| 0 | 2018-01-02 |
| 1 | 2018-01-03 |
| 2 | 2018-01-04 |
| 3 | 2018-01-05 |
| 4 | 2018-01-08 |
| … | … |
| 1116 | 2021-12-27 |
| 1117 | 2021-12-28 |
| 1118 | 2021-12-29 |
| 1119 | 2021-12-30 |
| 1120 | 2021-12-31 |
では, いよいよ予測パートです. predict に予測したい期間を含んだ future データフレームを渡して予測を行います.
pred = model.predict(future)
fig_pred = model.plot(pred)黒点が観測値で, 観測値がない未来の期間(グラフ右側)の青線部分が予測値となります. 水色の範囲は誤差の範囲を表しています.
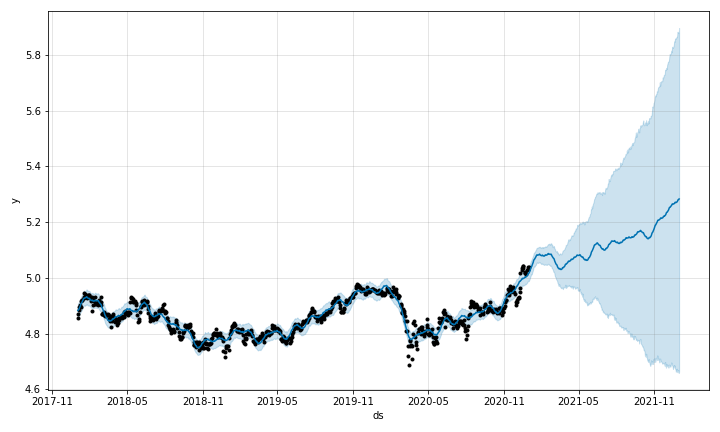
トレンドや周期成分ごとのグラフを描画することもできます. 10月末あたりが買いのようだ!
fig_components = model.plot_components(pred)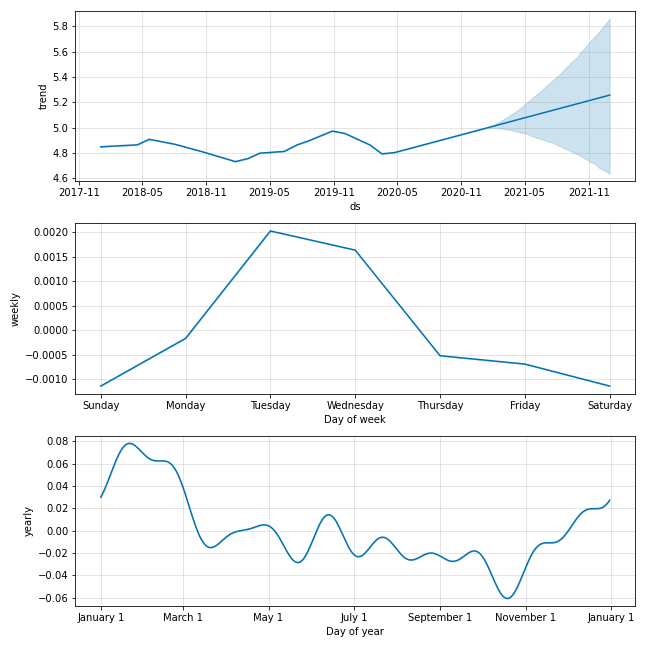
ちゃんと予測できているのか?
先程得られた予測モデルに, 2021年1月以降のデータを重ねてみて実際に株価の値動きが予測できているか簡単に確かめてみます.
start = datetime.date(2021,1,1)
end = datetime.date(2021,11,1)
data_test = DataReader('TM', 'yahoo', start, end)
data_test['ds'] = data_test.index
data_test = data_test.rename({'Adj Close':'y'} ,axis=1)
data_test['y'] = np.log(data_test['y'])
model = Prophet()
model.fit(data_test)
fig_test = model.plot(pred)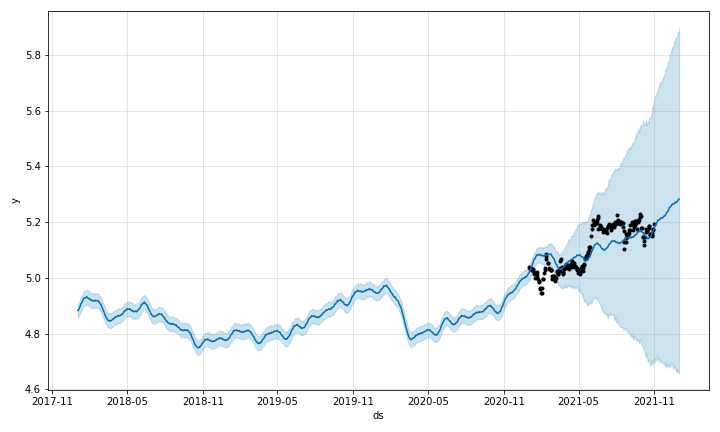
上昇トレンドは捉えられているようです. 5月前半からの6月にかけて予測以上の成長を見せていますが, これはトヨタの決算発表が要因みたいですね.
トヨタは5月12日に発表した決算で、今期の営業利益が前期比14%増の2兆5000億円などとする見通しを公表。コロナや世界的な半導体不足などの影響で自動車生産に影響が続き、競合の日産自動車は収支とんとんの見通しを示す中で強さを示した。
このように, 株価は外乱の影響を受けまくるので, 過去の株価だけから値動きを予測するのは不可能だと言われていますが, 今回はたまたま上手く予測できまみたいです. やったね!
Comments are closed