敷き詰めパズル「ペントミノ」をPULPで解いてみる

はじめに

以前、敷き詰めパズルのペントミノを量子コンピュータで解いてみようとしたところ、なかなか解が出なくて大変だったので、同じ問題をPULPで組合せ問題として解いたらどうなるかやってみようと思います。

問題

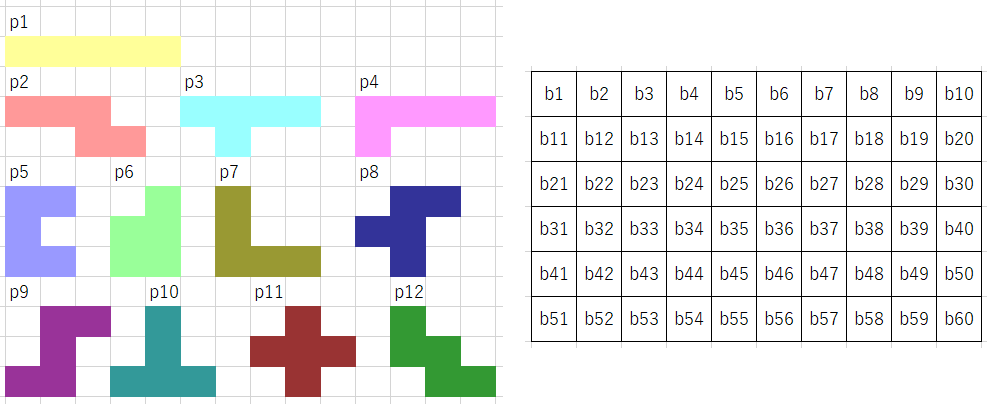
ペントミノとは、５つの正方形を組み合わせた形状のことで、下図左の１２個のピースがあります。ピースは、回転したり、裏返したりすることができます。
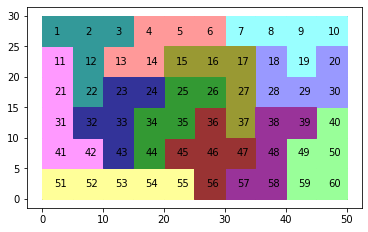
これらのピースを、下図右のようなボートに敷き詰めていきます。

考え方

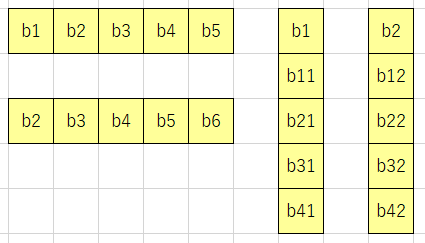
まずはピースp1のボードへの置き方を考えてみます。例えば、横向きにb1,b2,b3,b4,b5のところに置く、それを右に１つずらしてb2～b6のところに置く、などのような置き方が考えられます。
また、縦向きにして、b1,b11,b21,b31,b41のところに置く、というような置き方も考えられます。
横向きにしておく置き方が36パターン、縦向きにしておく置き方が20パターン、全部で56パターンあるようです。これらの置き方すべてを列挙し、それぞれprb[0][]=[1,2,3,4,5],prb2=[2,3,4,5,6]・・・のような配列に入れておきます。
prb[0][0]=[1,2,3,4,5] ：ピース１（配列では0になっていますが）の置き方0は、ボードの「1,2,3,4,5」の部分をカバーする、というような意味です。

同様にしてすべての12ピースについて置き方を列挙します。
ピースによっては、例えばp8のピースでは、回転と反転で８パターンあり、さらにボードへの置き方があるので、置き方の組合せもたくさんあります。

もちろん、すべて手作業で列挙するのは大変ですから、例えばp2のピースを

[[1, 1, 1, 0], [0, 0, 1, 1]]

のような配列で表して、プログラムで回転・反転・置き方を計算しました。
ボードへの置き方では、例えばピースp11をボードの隅に置くような置き方は意味がありませんが、そのような置き方もすべて列挙しました。そのような置き方は、最適化計算で弾かれるはずだからです。

立式

PULPで数式化します。
パズルなので、最小化・最大化する問題ではなく、すべて制約条件で書きます。

■制約条件１
１つ目の制約条件は、各ピースの置き方の中から１のみが選ばれる、という制約条件です。例えばピース１は置き方が56パターンありますが、その中から１つの置き方のみが選ばれないといけません。
それぞれの置き方が採用された場合１，採用されなかった場合０となるようなバイナリー変数で以下のように立式します。

_C1: x_0_0 + x_0_1 + x_0_10 + x_0_11 + x_0_12 + x_0_13 + x_0_14 + x_0_15
 + x_0_16 + x_0_17 + x_0_18 + x_0_19 + x_0_2 + x_0_20 + x_0_21 + x_0_22
 + x_0_23 + x_0_24 + x_0_25 + x_0_26 + x_0_27 + x_0_28 + x_0_29 + x_0_3
 + x_0_30 + x_0_31 + x_0_32 + x_0_33 + x_0_34 + x_0_35 + x_0_36 + x_0_37
 + x_0_38 + x_0_39 + x_0_4 + x_0_40 + x_0_41 + x_0_42 + x_0_43 + x_0_44
 + x_0_45 + x_0_46 + x_0_47 + x_0_48 + x_0_49 + x_0_5 + x_0_50 + x_0_51
 + x_0_52 + x_0_53 + x_0_54 + x_0_55 + x_0_6 + x_0_7 + x_0_8 + x_0_9 = 1

これをすべてのピースについて制約します。
12ピースそれぞれ、１つの置き方のみが選ばれる制約条件になります。

■制約条件２
２つ目の制約条件は、ボード上でピースが重ならないようにする、というものです。
例えば、ピース１の置き方として、[1,2,3,4,5]、ピース6の置き方として[2,11,12,21,22]という置き方が考えられますが、この２つが採用されるとボード上の２の部分が重なってしまいますのでダメです。
そのため、「ボード上の同じ場所に置かれるような置き方から１つのみを選ぶ」というのを制約条件を設定します。
例えばボードb1に関する式は以下のようになっています。

_C13: x_0_0 + x_0_36 + x_10_0 + x_10_60 + x_11_0 + x_11_145 + x_1_0 + x_1_120
 + x_1_154 + x_1_180 + x_1_34 + x_1_94 + x_2_0 + x_2_116 + x_2_149 + x_2_33
 + x_3_0 + x_3_149 + x_3_207 + x_3_58 + x_4_0 + x_4_113 + x_4_148 + x_4_187
 + x_4_222 + x_4_39 + x_5_0 + x_5_32 + x_6_0 + x_6_31 + x_6_93 + x_7_0
 + x_7_90 + x_8_0 + x_8_30 = 1

これを、ボードb1～b60すべてのセルについて制約します。

このようにして、全部で72の制約式で表現できました。

計算

PULPで解いてみます。

prob= pulp.LpProblem("pentomino",pulp.LpMinimize)
xs=[]
for i in range(len(prb)):
    x=[pulp.LpVariable('x_{}_{}'.format(i,j), cat='Binary') for j in range(len(prb[i]))]
    xs.append(x)
# 制約条件１
#１つのピースの中では、置き方を１つだけ選択できる
for i in range(len(xs)):
    prob += pulp.lpSum(xs[i]) == 1
# 制約条件２
#盤面に重ならないように配置する
for i in range(1,61):
    bs=[]
    for j,itemj in enumerate(prb):
        for k,itemk in enumerate(itemj):
            if i in itemk: bs.append(xs[j][k])
    prob+=pulp.lpSum(bs) == 1
#PULPで解く
solver=pulp.PULP_CBC_CMD()
status=prob.solve(solver)
#解を取得
ans=[]
for xs1 in xs:
    ans_bin=[x.value() for x in xs1]
    ans.append([i for i in range(len(ans_bin)) if ans_bin[i]==1])   

このようにすると、解として

[[30], [42], [122], [117], [295], [71], [105], [59], [0], [25], [48], [103]]

が選ばれました。ピース１は30番目の置き方、ピース２は42番目の置き方、ピース3は122番目の置き方・・・が選ばれているようです。

結果

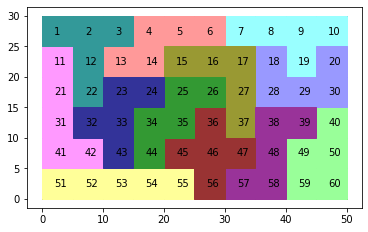
図にすると以下のように解けていることが分かりました。
計算自体は一瞬で終わっていました。PULPにはとても簡単な問題だったようです。

まとめ

ペントミノは、アルゴリズムで解くやり方がいろいろ提案されているようです。
ボードの隅からピースを１つずつ詰めて行って、置けなくなったら１つずつ戻って戻ったところからまた進める、というようなやり方が多いようです。
解はもちろん１つではなくて、いろいろな解があるのですが、すべての解を列挙するのに〇〇分かかった、というような記事があったりします。
PULPで上記のようにやると、毎回同じ解しか出てこないのですが、すべての解を列挙するような立式も考えられるかもしれません。